asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,225
- Gender
- Undisclosed
- HSC
- 2012
I'm assuming that means sit snugly inside the parabola? OMG I JUST SOLVED IT!! SO HAPPY WTF OMG HAHHAHAHAHA. I feel...so smart...yet among some of these questions...
The general equation of a circle is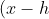^2+(y-k)^2=r^2) . Here
. Here 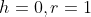 . Solving simultaneously the parabola and circle,
. Solving simultaneously the parabola and circle, ^2=1\\y^2+y(1-2k)+k^2-1=0) . As the solution is a double root, the discriminant equals 0.
. As the solution is a double root, the discriminant equals 0. ^2-4(k^2-1)=0) .
. 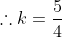 . The circle has centre
. The circle has centre ) .
.
By a similar process, the centre of the circle in the parabola is
is ) (Different k to top one)
(Different k to top one)
The general equation of a circle is
By a similar process, the centre of the circle in the parabola
Last edited:



