-
Looking for HSC notes and resources? Check out our Notes & Resources page
HSC 2013 MX2 Marathon (archive) (8 Viewers)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
i) All variables within S_k is positive, all operations are positive, hence S_k > 0
 < \frac{a}{k} \left(\frac{1}{n} + \frac{1}{n} + \dots + \frac{1}{n} \right) = \frac{a}{k} )
ii) Consider the upper and lower rectangle of the curve y=1/x, from x=t and x=t+b
iii) Consider the lower bound and the middle term for (ii)
Substitute, t=kn, t=kn+b, t=kn+2b, ... , t=kn+(n-1)b, add them all side by side:

Take the upper bound and middle term for (ii)
Substitute, t=kn+b, t=kn+2n, ... , t=kn+nb, and add them side by side, note that the logarithms telescope and cancel out
 + b}{kn+b} )
Then make the inequality into one whole one with b/a S_n in the middle, multiply everything by a/b to yield what is needed. Then taking the limit to infinity, makes the lower bound converge to the upper bound, by the squeeze theorem the middle term then becomes the upper and lower bound's limit.
 )
iii)
Integrate both sides from 0 to 1. Both are positive over this interval.
iv) (iii), proves that the error integral in (ii) converges to zero as n approaches infinity (by squeeze theorem in part (iii). Hence as n approaches infinity, for part (ii) the integral converges to zero and the sum remains.
v) general inductive proof, we do not refer to the lower bound in this proof, because due to the infinite series in iv)
!} + \frac{1}{(n+2)!} + \dots > \frac{1}{(n+1)!} ) by default since all terms are positive.
by default since all terms are positive.
The upper bound is proven by induction, by using the infinite series in the assumed step, then subtracting 1/(m+1)! to both sides of the upper bound inequality.
vi) From what is proven in part (v), multiply everything by n!. The sum in the middle becomes a series of integers, hence is N.
viii) Let e=p/q, p and q are integers, since p and q are integers and n! = n(n-1)(n-2)(n-3)....(q)....(3)(2)(1). n! is divisible by q and hence p/q n! is an integer.
But since N is an integer therefore p/qn! - N is an integer, BUT the lower bound is 1/(n+1) < 1 and the upper bound is 1/n < 1. Therefore the middle CANNOT be an integer.
Hence a contradiction has arisen due to letting e=p/q
Therefore by proof by contradiction, e is irrational.
i) All variables within S_k is positive, all operations are positive, hence S_k > 0
ii) Consider the upper and lower rectangle of the curve y=1/x, from x=t and x=t+b
iii) Consider the lower bound and the middle term for (ii)
Substitute, t=kn, t=kn+b, t=kn+2b, ... , t=kn+(n-1)b, add them all side by side:
Take the upper bound and middle term for (ii)
Substitute, t=kn+b, t=kn+2n, ... , t=kn+nb, and add them side by side, note that the logarithms telescope and cancel out
Then make the inequality into one whole one with b/a S_n in the middle, multiply everything by a/b to yield what is needed. Then taking the limit to infinity, makes the lower bound converge to the upper bound, by the squeeze theorem the middle term then becomes the upper and lower bound's limit.
ii) Make f(t) = e^t. Then simplify out, once integral is simplified, sub in x=1.If you don't mind me expanding on this
 Hence prove that$ \ \ e \ \ $is irrational$ \ \ \ \ \fbox{2} )
iii)
Integrate both sides from 0 to 1. Both are positive over this interval.
iv) (iii), proves that the error integral in (ii) converges to zero as n approaches infinity (by squeeze theorem in part (iii). Hence as n approaches infinity, for part (ii) the integral converges to zero and the sum remains.
v) general inductive proof, we do not refer to the lower bound in this proof, because due to the infinite series in iv)
The upper bound is proven by induction, by using the infinite series in the assumed step, then subtracting 1/(m+1)! to both sides of the upper bound inequality.
vi) From what is proven in part (v), multiply everything by n!. The sum in the middle becomes a series of integers, hence is N.
viii) Let e=p/q, p and q are integers, since p and q are integers and n! = n(n-1)(n-2)(n-3)....(q)....(3)(2)(1). n! is divisible by q and hence p/q n! is an integer.
But since N is an integer therefore p/qn! - N is an integer, BUT the lower bound is 1/(n+1) < 1 and the upper bound is 1/n < 1. Therefore the middle CANNOT be an integer.
Hence a contradiction has arisen due to letting e=p/q
Therefore by proof by contradiction, e is irrational.
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,225
- Gender
- Undisclosed
- HSC
- 2012
Re: HSC 2013 4U Marathon
I'm guessing you're not looking for a proof by induction?
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
If I want an inductive solution, I will specify that in the question
Yep.I'm guessing you're not looking for a proof by induction?
If I want an inductive solution, I will specify that in the question
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon

My first thought is to construct an infinite product that actually equals to . The most simple form would be:
. The most simple form would be:

Multiplying all the 2's together will add the powers to get:

Now for this to equal , we want:
, we want:

The easiest way to do this is to let:
 such that:
such that:

So we get the infinite product:

Which in expanded terms is:

Now lets consider what we can do with this infinite product:
1) Since all terms are less than 1, then by multiplying by an extra term decreases the actual product each time. Hence the product will be a minimum when there are infinite terms.
2) Since the product is a minimum when there are infinite terms, then all we have to do is show that the infinite product of the result that needs to be proven is larger than the infinite product we constructed.
Now trying to figure out how to finish this off...
If you simplify the LHS, it becomes:
My first thought is to construct an infinite product that actually equals to
Multiplying all the 2's together will add the powers to get:
Now for this to equal
The easiest way to do this is to let:
So we get the infinite product:
Which in expanded terms is:
Now lets consider what we can do with this infinite product:
1) Since all terms are less than 1, then by multiplying by an extra term decreases the actual product each time. Hence the product will be a minimum when there are infinite terms.
2) Since the product is a minimum when there are infinite terms, then all we have to do is show that the infinite product of the result that needs to be proven is larger than the infinite product we constructed.
Now trying to figure out how to finish this off...
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon

Maybe using calculus, taking f(x) = LHS - RHS, then differentiating etc etc.
But differentiating the RHS would be..... yeah lol
EDIT: I guess logarithmic differentiation would be good. But I'll let you continue.
Its an interesting solution though.
Quite clever, I'm unsure about how to prove that:If you simplify the LHS, it becomes:
My first thought is to construct an infinite product that actually equals to. The most simple form would be:
Multiplying all the 2's together will add the powers to get:
Now for this to equal, we want:
The easiest way to do this is to let:
such that:
So we get the infinite product:
Which in expanded terms is:
Now lets consider what we can do with this infinite product:
1) Since all terms are less than 1, then by multiplying by an extra term decreases the actual product each time. Hence the product will be a minimum when there are infinite terms.
2) Since the product is a minimum when there are infinite terms, then all we have to do is show that the infinite product of the result that needs to be proven is larger than the infinite product we constructed.
Now trying to figure out how to finish this off...
Maybe using calculus, taking f(x) = LHS - RHS, then differentiating etc etc.
But differentiating the RHS would be..... yeah lol
EDIT: I guess logarithmic differentiation would be good. But I'll let you continue.
Its an interesting solution though.
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,662
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
\right)\left(\displaystyle\prod_{k=2}^n (k+1)\right)}{(n!)^2}=\frac{n+1}{2n}>\frac{1}{2}.)
(added in mark count as an estimated length of soln)
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
 we are allowed to do this since order in multiplication does not matter.
we are allowed to do this since order in multiplication does not matter.
The seperate products all cancel out if you expand it out to yield n+1/2n > 1/2
Similar to what I had in mind:
The seperate products all cancel out if you expand it out to yield n+1/2n > 1/2
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
 (\frac{1}{x_1} + \frac{1}{x_2} + \dots + \frac{1}{x_n}) \geq n^2 )
This can be done by expanding the LHS, you will get, an n number of 1's
And pairs of reciprocals, i.e. x1/x2 + x2/x1, an nC2 number of these pairs
pairs of reciprocals, i.e. x1/x2 + x2/x1, an nC2 number of these pairs
And we know that:

That means in the above expression:

proof is then complete.
LHS - RHS, make it a common denominator, the result simplifies into proving:
(don't feel the obligation to answer the questions I'm posting in order, answer whichever ones you want to)
This can be done by expanding the LHS, you will get, an n number of 1's
And
And we know that:
That means in the above expression:
proof is then complete.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,662
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
(and gives you the equality condition of all numbers being equal).LHS - RHS, make it a common denominator, the result simplifies into proving:
This can be done by expanding the LHS, you will get, an n number of 1's
Andpairs of reciprocals, i.e. x1/x2 + x2/x1, an nC2 number of these pairs
And we know that:
That means in the above expression:
proof is then complete.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Coming from x_k/x_(k+1) = x_(k+1)/x_k, and x_k is positive. Hence x_k=x_(k+1)
Oops yeah hehe.(and gives you the equality condition of all numbers being equal).
Coming from x_k/x_(k+1) = x_(k+1)/x_k, and x_k is positive. Hence x_k=x_(k+1)
Makematics
Well-Known Member
Re: HSC 2013 4U Marathon
soz to kill the party but does anyone have any harder Q's on topics other than Harder 3 unit? i mean it is the HSC 4U Marathon after all!
soz to kill the party but does anyone have any harder Q's on topics other than Harder 3 unit? i mean it is the HSC 4U Marathon after all!
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
I think this counts under Polynomials:soz to kill the party but does anyone have any harder Q's on topics other than Harder 3 unit? i mean it is the HSC 4U Marathon after all!
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,662
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
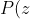=Q(z)(z^2+1)+(z^2-z+1)\\ \Rightarrow \sum_{n=1}^4 P(z_n)=\sum_{n=1}^4 z_n^2 -\sum_{n=1}^4 z_n +4\\=(\sum_{n=1}^4 z_n)^2-2\sum_{m<n}z_mz_n - \sum_{n=1}^4 z_n +4 = 6.)
As no-one else seems to be answering it:I think this counts under Polynomials:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon


Where r is the radius, and theta is the angle the particle makes with the x-axis at some time t. And x and y are the x and y displacements with respect to the origin on a cartesian plane.
Now differentiate with respect to t





Then differentiate again, BUT:

Because I haven't specified non-uniform circular motion, merely circular motion, therefore, when we differentiate again, we cannot take omega as constant, and hence must use product rule
 )
 )
Now, we know that in Physics, centripetal acceleration, which is (a), is towards the centre of the circular motion.

Substitute the and
and  that was in terms of theta, phi and omega into this equation.
that was in terms of theta, phi and omega into this equation.
And you will in the end arrive at the above answer.
(Note that if we assume uniform circular motion, then phi = 0, and we arrive at the familiar formula a=rw^2 )



Multiply all inequalities together to get the answer.
b)
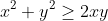


Add all inequalities side by side:
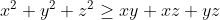
Substitute:

(ac) + (ab)(bc) + (ac)(bc) = abc(a+b+c) )
And c) asianese answered that.
First lets model the particle travelling in circular motion with parametric equations:Here is a mechanics one:

Where r is the radius, and theta is the angle the particle makes with the x-axis at some time t. And x and y are the x and y displacements with respect to the origin on a cartesian plane.
Now differentiate with respect to t
Then differentiate again, BUT:
Because I haven't specified non-uniform circular motion, merely circular motion, therefore, when we differentiate again, we cannot take omega as constant, and hence must use product rule
Now, we know that in Physics, centripetal acceleration, which is (a), is towards the centre of the circular motion.
Substitute the
And you will in the end arrive at the above answer.
(Note that if we assume uniform circular motion, then phi = 0, and we arrive at the familiar formula a=rw^2 )
a) (I should of specified that a > 0, b > 0, c > 0)Just some inequalities, they are not in order of difficulty, nor will the answer to one necessarily help with the others:
$ \ \ \frac{a+b+c+d}{4} \geq \sqrt[4]{abcd} )
Multiply all inequalities together to get the answer.
b)
Add all inequalities side by side:
Substitute:
And c) asianese answered that.
Last edited:
- Status
- Not open for further replies.
