Alright, here we go:
First we establish that our flips can be expressed in a string of Hs and Ts representing Heads and Tails respectively. The structure of this string will have to be:
_ _ _ _ _ ...... _ T H H H H .... H
Note, that is an 'n' number of Hs in the end of this string, we need a T before it to start the "streak" of Hs in the end, the rest is arbitrary (with some restrictions**), totaling an 'm' number of digits in our string.
**The restrictions come about when the number of remaining spots to fill 'm-n-1' spots is greater than or equal to 'n'. Since this gives rise for a chance for the streak of n Hs to be established before the 'm' moves have happened.
So now we establish the necessary domains for p_m to evaluate it
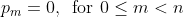
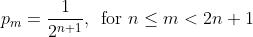
The first is clear, the second is since there are only (n+1) slots that are fixed for each string (the end ones as illustrated in the first example). The rest of the slots can be filled arbitrarily.
Now the difficult one is to consider is when

It comes down to finding
 = \ $probability that a streak of$ \ n \ $H's cannot be established within this string$ = 1- P($that there is a streak of$ \ n \ $H's in$ \ m-n-1) )
 = 1 - \frac{2^{m-2n}}{2^{m-n-1}} = 1 - \frac{1}{2^{n-1}} )
p_{n+1} + \dots + 2n p_{2n} + (2n+1)p_{2n+1} + \dots )
 )
And if my calculations are correct this diverges, what have I done wrong?
