rand_althor
Active Member
- Joined
- May 16, 2015
- Messages
- 554
- Gender
- Male
- HSC
- 2015
Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread
 \\y-0&=a(a-b)(x-a) \\y&=a(a-b)(x-a) \\\textup{Tangent at }x=b: \\y-y_1&=m(x-x_1) \\y-0&=-a(a-b)(x-b) \\y&=-a(a-b)(x-b) \\\textup{Equating tangents to find M:} \\a(a-b)(x-a)&=-a(a-b)(x-b) \\x-a&=-x+b \\2x&=a+b\\x&=\frac{a+b}{2}\end{align*})
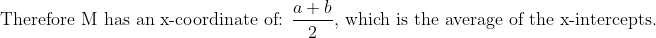
Last edited:

Not sure what you mean by this.But why is the boundary point which = local maxima ??
Are boundary points excluded??
Q4
Find i) the local maxima or minima and ii) the global maximum and minim of the funciton y = x^4 -8x^2 + 11 on each of the domains:
a) 1 less than or equal to x less than or equal to 3.
I have found the global max = 11 and global min = 4
But why is the boundary point which = local maxima ??
Are boundary points excluded??
They asked for the local and global extrema on the domain 1 ≤ x ≤ 3. So we only focus on the curve in this domain, in other words, sketch only the emboldened part of rand_althor's graph.
Global maximum: No global maximum as the curve approaches ∞ as x approaches ∞ and -∞.
Global minimum: f(x)=-5 when x=2 or -2.
Local maximum: f(x)=20 when x=3.
Local minimum: f(x)=-5 when x=2.
Not sure what you mean by this.
Ah okay, apologies for the wrong answers appleibeats.They asked for the local and global extrema on the domain 1 ≤ x ≤ 3. So we only focus on the curve in this domain, in other words, sketch only the emboldened part of rand_althor's graph.
So the answers are:
Global maximum: 20 (obtained at the endpoint x = 3).
Global minimum: -5 (obtained at x = 2 )
Local maximum: none in the domain
Local minimum: -5 (obtained at x = 2).
For x > 0.
Yes.Is this correct for x<0?
}} \\ &=\frac{x}{|x|\sqrt{1+\frac{1}{x^2}}} \\&=\frac{x}{-x\sqrt{1+\frac{1}{x^2}}} \\&=-\frac{1}{\sqrt{1+\frac{1}{x^2}}}\end{align*})

