Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread
proof by induction: n(n+1)(n+2) is divisible by 3 for all integers greater than or equal to 1
prove that 7^n+3n(7^n)-1 is divisible by 9 for all positive numbers n
prove that 5^n > n^5
Answer to the 1st part of your question:
Theorem: If n is a positive integer, then n(n+1)(n+2) is divisible by 3
Proof by induction:
n=1
1*2*3 = 6, which is divisible by 6.
Assume that for n = k, k(k+1)(k+2) is divisible by 6
We need to show that, based on that assumption, (k+1)(k+2)(k+3) is also
divisible by 6.
(k+1)(k+2)(k+3) = (k+1)(k+2)k + (k+1)(k+2)3 = k(k+1)(k+2) + 3(k+1)(k+2).
By induction hypothesis, the first term is divisible by 6,
and the second term 3(k+1)(k+2) is divisible by 6 because it contains
a factor 3 and one of the two consecutive integers k+1 or k+2 is
even and thus is divisible by 2. Thus it is divisible by both 3 and
2, which means it is divisible by 6. The theorem is proved since
the sum of two multiples of 6 is also a multiple of 6.
 \;\textup{for nothing. There is no such thing as a free lunch.})
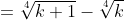
(\sqrt[4]{k}+\sqrt[4]{k+1})} )
