Thanks! If you don't mind, could you also give a proof for this one InteGrand?
So the ellipse condition is that the point
P on the (upper-half of the) ellipse has
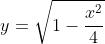
.
The squared distance as a function of
x is then
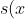 = (x-a)^2 + 1-\frac{x^2}{4})
.
This can be differentiated to help find the minimum:
 = 2(x-a)-\frac{2x}{4}=2(x-a)-\frac{x}{2}=\frac{3}{2}x-2a)
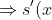 = 0 \text{ when }\frac{3}{2}x-2a=0\Leftrightarrow x=\frac{4a}{3})
.
So the minimal squared distance is
^2 + 1 - \frac{\left(\frac{4a}{3} \right)^2}{4}=\frac{1}{3}(3-a)^2 = 1 - \frac{a^2}{3})
From simplifying this, you get the top part of the answer you posted.
To see the reason for the split in answers for different values in
a, note that
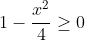
(since it's under a square root). Substituting
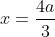
yields
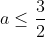
in order for the top half of the answer to be feasible. In other words, we need -2 ≤ x ≤ 2 for the point to be on the ellipse and make sense, but if a > 3/2, this no longer happens, as x becomes bigger than 2.
(For
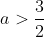
, the point on the ellipse we worked out as being closest, namely
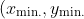 =\left(\frac{4a}{3},\sqrt{1-\frac{\left(\frac{4a}{3}\right)^2}{4}}\right) )
, is no longer a real point, which is why we need the condition on
a.)
To see why using
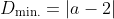
when
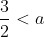
is optimal, note that the squared distance function represents a concave up parabola. Therefore, it is minimised at its vertex, and as we saw before, this globally minimising
x-value is
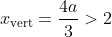
as
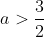
. So the parabola is minimised at a point x
vert. where x
vert. > 2, so the closest we can get to this minimal value by taking a point on the ellipse (where x needs to be less than 2) is to make
x closest to x
vert.. To make x closest to x
vert. and have x be on the ellipse, we need to take x = 2, as x
vert. > 2. This point (the point (2,0)) on the ellipse has distance to the point (
a, 0) of
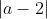
as required.
(
So basically I'm saying that if a quadratic is minimised at an x-value of xvert., if we are restricted to x-values less than some maximal allowable value X, then the minimal attainable value for the quadratic is its value at this X (because the quadratic will be monotone decreasing on (-∞, X], as X < xvert.). In our case, the maximal allowable value of X is X = 2 (this constraint coming from the ellipse). So taking x = 2 gives us the place of the min.)
Edit: Realised I didn't prove the maximal distance part. But this part is easier than the minimal part, so I'll leave it as an exercise for the reader.

