Paradoxica
-insert title here-
If you accept Stirling's Inequality:This obviously converges but the ratio test is inconclusive, so how would you justify it
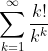
The root test gives convergence of the RHS, thus giving convergence of the LHS.
If you accept Stirling's Inequality:This obviously converges but the ratio test is inconclusive, so how would you justify it
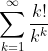
Check your calculations, the ratio test is conclusive. (The ratio tends to exp(-1).)This obviously converges but the ratio test is inconclusive, so how would you justify it
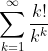
Could you use something like this?This obviously converges but the ratio test is inconclusive, so how would you justify it
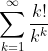

Huh?Could you use something like this?

According to a quick evaluation in Mathematica, the two integrals provided above have opposite signs.
Because say we swap the rows, then the determinant becomes +2. But it still "looks like" a Jacobian.

I believe we multiply by the absolute value of the Jacobian in a change of variable substitution.Only adds to confusion really because I wouldn't know where the mistake is.
I legit did not know that about the abs. valueI believe we multiply by the absolute value of the Jacobian in a change of variable substitution.
Btw, when did we learn this change of variable substitition in 1251? Didn't see any questions on it.
lol it depends on the lecturer, mine always called them YacobiansI legit did not know that about the abs. value
Also, this was Q124 of the calculus pack. And yes we had a lecture on Jacobians; I think it was the second last one.
The sequence is strictly less than n-n
I want to use the alternating series test to show that this is conditionally convergent (it already fails absolute convergence). It's clear that the relevant terms will be positive and I can prove that they limit off to 0, but how do I prove that

Yeah I'll buy that if nobody comes with a better ideaThe sequence is strictly less than n-n
I guess you could work on that instead.
It's decreasing because the denominator is increasing. The denominator is increasing because
I want to use the alternating series test to show that this is conditionally convergent (it already fails absolute convergence). It's clear that the relevant terms will be positive and I can prove that they limit off to 0, but how do I prove that

