86??? Stop coping just because you did bad, I’d say more like 96
Maths Extension 2 Predictions/Thoughts (2 Viewers)
- Thread starter carrotsss
- Start date
synthesisFR
afterhscivemostlybeentrollingdonttakeitsrsly
ay dont be like that bro got 4/10 for mcq
he would have to ace the rest of the paper and still not get itscaryshark09
∞∆ who let 'em cook dis long ∆∞
- Joined
- Oct 20, 2022
- Messages
- 1,618
- Gender
- Undisclosed
- HSC
- 1999
my friends were hyping my up for mc cause i always got 9-10 in every paper both 3u and 4uay dont be like that bro got 4/10 for mcq
scaryshark09
∞∆ who let 'em cook dis long ∆∞
- Joined
- Oct 20, 2022
- Messages
- 1,618
- Gender
- Undisclosed
- HSC
- 1999
but hey, someone got 3/10 in mc last year at my school and they got 99.85 atar
Nah stop that is so unrealistic, I’d say a 98
An incorrect view has been expressed that 15bii can't be done without the use of vectors.
Here is an alternative solution to 15bii without the use of vectors:
The sum of the squares of two pairs of opposite edges of a tetrahedron is equal to the sum of the squares of the remaining two opposite edges increased by four times the square of the bimedian relative to these last edges.
Altshiller-Court, N. Modern Pure Solid Geometry. New York: The Macmillan Company 1935, page 56.
As a corollary, the sum of the squares of the edges of a tetrahedron is equal to four times the sum of the squares of its bimedians.
Here is an alternative solution to 15bii without the use of vectors:
The sum of the squares of two pairs of opposite edges of a tetrahedron is equal to the sum of the squares of the remaining two opposite edges increased by four times the square of the bimedian relative to these last edges.
Altshiller-Court, N. Modern Pure Solid Geometry. New York: The Macmillan Company 1935, page 56.
As a corollary, the sum of the squares of the edges of a tetrahedron is equal to four times the sum of the squares of its bimedians.
Last edited:
And here is yet another non-vector proof which is even older (although not as elegant as Altshiller-Court's):
From The American Mathematical Monthly, Vol. 25 Issue 3, page 122 (1918)
Note that the theorem they are referring to is Apollonius' Theorem. This is in the Cambridge Extension 1 Year 12 Chapter 8 Review Exercise Q14 page 427 (although not named as such there) as well as in the Cambridge Maths Extension 1 HSC Practice Examination Q14a (wherein they give it the proper name). Although those use vector methods there is a non-vector proof at https://en.wikipedia.org/wiki/Apollonius's_theorem
From The American Mathematical Monthly, Vol. 25 Issue 3, page 122 (1918)
Note that the theorem they are referring to is Apollonius' Theorem. This is in the Cambridge Extension 1 Year 12 Chapter 8 Review Exercise Q14 page 427 (although not named as such there) as well as in the Cambridge Maths Extension 1 HSC Practice Examination Q14a (wherein they give it the proper name). Although those use vector methods there is a non-vector proof at https://en.wikipedia.org/wiki/Apollonius's_theorem
Last edited:
Taking a rather more sophisticated approach we may get another proof without vectors - using a generalisation found in 2013.
First redefine the term bimedian for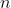
points as the segment joining the midpoint of one segment to the barycenter of the remaining 
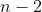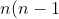points. Then the sum of the squares of the /2)
bimedians is equal to )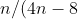
times the sum of the squares of all segments joining the 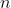points.
In the case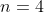
, the six bimedians coincide two by two. This explains why, in this case, we now have one half of the sum of the squares of its edges, instead of one fourth.
Fonda, A., On a Geometrical Formula Involving Medians and Bimedians, Mathematics Magazine, Vol. 86, No. 5 (December 2013), pp. 351-357
First redefine the term bimedian for
In the case
Fonda, A., On a Geometrical Formula Involving Medians and Bimedians, Mathematics Magazine, Vol. 86, No. 5 (December 2013), pp. 351-357
So now the solutions at https://4unitmaths.com/hsc2023e2-tywebb.pdf have been updated to include the Altshiller-Court, Apollonius of Perga and Fonda methods for 15bii.
Date has been set for the 2024 HSC Feedback Day for NESA presentations on marking of the 2023 HSC Maths exams
9am-4:30pm on Feb 24, 2024. Venue TBC.
Hopefully they will do video recordings instead of the audio ones they did this year.
I will post again later when I know the venue.
9am-4:30pm on Feb 24, 2024. Venue TBC.
Hopefully they will do video recordings instead of the audio ones they did this year.
I will post again later when I know the venue.
Terry Lee Solutions: https://advancedmathematics.com.au/Resources/2023 Ext2.pdf
I found out it is at the same place as last year, but not whether the recordings will be video/audio only. Last year it was audio only and views were expressed that it would have been better to do videos.
UTS - Guthrie Theatre Building 6,
702 Harris Street
Ultimo
9am-10:30am: Extension 2
10:55am-12:05pm: Extension 1
12:50pm-2:25pm: Advanced
2:45pm-4:30pm: Standard 1 and 2
- Presented by Senior Markers of the 2023 HSC Mathematics examinations.
- Syllabus areas where students displayed strength of understanding and competence in the application of skills will be highlighted. Areas where students experienced lack of knowledge, skills and understanding will also be discussed.
- Participants will be given advice to strengthen students’ ability to write coherent solutions under examination conditions.
Last edited:
You going?
It has been confirmed that audio recordings will be made. Last year the audio recordings were accompanied with the slides too.
So I don't think I'll go. I'll wait for the audio recordings and slides. But I still think videos would be better. They only ever did that during the covid lockdowns
It has been confirmed that audio recordings will be made. Last year the audio recordings were accompanied with the slides too.
So I don't think I'll go. I'll wait for the audio recordings and slides. But I still think videos would be better. They only ever did that during the covid lockdowns
Last edited:
Ext. 2 recording: https://www.mediafire.com/file/twgdyon9n6oowot/e2-nesa-presentation-2023hsc.zip/file
It comes with mp3 and pdf of slides.
I'll put the others up later.
It comes with mp3 and pdf of slides.
I'll put the others up later.
Here are the others for ext 2, ext 1, adv, std 1 and std 2:
This has all 4 mp3s and pdfs so is much larger than the other one:
note that the standard 1 and 2 are combined
This has all 4 mp3s and pdfs so is much larger than the other one:
note that the standard 1 and 2 are combined