Here's how to see the function is always positive in the given domain:
If
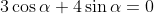
, then dividing through by cos
α (which we can do because we know
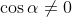
for
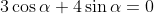
, because if
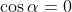
, then sin
α equals either 1 or -1, and neither of these makes
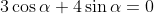
)

.
This is not true for any
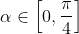
, since the tan function is positive or 0 in this domain. So the function never crosses the
y-axis in this domain.
So we just need to see whether the function's graph is above, or below, the
y-axis. We find that at
x = 0, the function equals 3, which is positive. So the function's graph is always above the
x-axis in the domain of integration (i.e. function always positive here, so the integral also gives us the area under the curve).