In order to let you work on the solution yourself, I will offer one based on a different identity:
^n\left(1 + \cfrac{1}{x}\right)^n = (1 + x)^{2n})
^n\left(1 + \cfrac{1}{x}\right)^n \\ &= (1+ x)^n\left[x^n\left(1 + \cfrac{1}{x}\right)^n\right] \\ &= (1+ x)^n\left[x\left(1 + \cfrac{1}{x}\right)\right]^n \\ &= (1+ x)^n\left(x + \cfrac{x}{x}\right)^n \\ &= (1+ x)^n(x + 1)^n \\ &= \left[(1+ x)^n\right]^2 \\ &= (1 + x)^{2n} \\ &=\ \text{RHS} \end{align*})
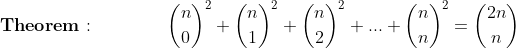
Considering the RHS of the identity established in the above Lemma, we can expand and see that:
^{2n} &= \binom{2n}{0} \times 1^{2n} \times x^0 + \binom{2n}{1} \times 1^{2n-1} \times x^1 + \binom{2n}{2} \times 1^{2n - 2} \times x^2 + ... + \binom{2n}{n} \times 1^{2n - n} \times x^n + ... + \binom{2n}{2n-1} \times 1^{2n - (2n -1)} \times x^{2n - 1} + \binom{2n}{2n} \times 1^{2n - 2n} \times x^{2n} \\ &= \binom{2n}{0} + \binom{2n}{1} x + \binom{2n}{2} x^2 + ... + \binom{2n}{n} x^n + ... + \binom{2n}{2n-1} x^{2n - 1} + \binom{2n}{2n} x^{2n} \end{align*})
It is clear that the term in
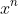
in this expansion is
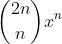
. Hence, the the term we seek for our result,
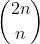
, is the coefficient of
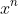
in the expansion of
^{2n})
. It is therefore reasonable to conjecture that the other part of the result we seek will be the coefficient of
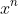
in the expansion of the LHS of the identity established in the Lemma.
Expanding the terms separately:
^n = \binom{n}{0} + \binom{n}{1} x + \binom{n}{2} x^2 + ... + \binom{n}{n-1} x^{n - 1} + \binom{n}{n} x^{n})
^n = \binom{n}{0} + \binom{n}{1} \cfrac{1}{x} + \binom{n}{2} \cfrac{1}{x^2} + ... + \binom{n}{n-1} \cfrac{1}{x^{n - 1}} + \binom{n}{n} \cfrac{1}{x^n})
Now, every term in the expansion of
^n\left(1 + \cfrac{1}{x}\right)^n)
will consist of the product of
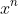
and a term from the first expansion and a term from the second expansion. Thus:
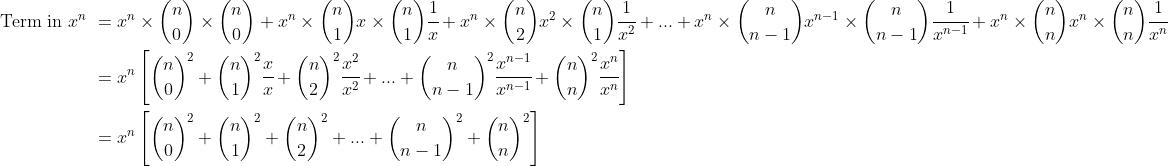
It thus follows from equating the coefficients of
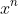
from the LHS and RHS of the identity established in the Lemma that we have found that:
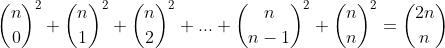
as expected.