Question 1
Find the surface area (to one decimal place)
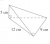
SA top = 1/2 x 9 x 12 = 54 cm^2
SA bottom = 1/2 x 9 x 12 = 54 cm^2
SA front = 1/2 x 12 x 5 = 30 cm^2
SA back = 1/2 x 15 x 5 = 37.5 cm^2 (used Pythagoras to get base of 15 cm)
Total SA= 175.5 cm^2
The actual answer says it is 180cm^2 (to one decimal place)
Question 2
Find the surface area (to one decimal place)
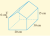
SA front = (1/2 x 20 x 6) + (20 x 15) = 360 cm^2
SA back = 360 cm^2
SA bottom = 30 x 20 = 600 cm^2
SA RHS = (30 x 15) + (11.66 x 30) used Pythagoras to find width of rectangle w^2 = 10^2 +6^2, w = 11.66 cm
= 799.86 cm^2
SA LHS = 799.86 cm^2
Total SA = 2919.7 cm^2 (to one decimal place)
The actual answer says it is 2819.2 cm^2 (to one decimal place)
Question 3
Find the surface area (to one decimal place)

SA RHS = 16.1 x 5.9 = 94.99 mm^2
SA LHS = 94.99 mm^2
SA front = 16.1 x 4 = 64.4 mm^2
SA back = 9.2 x 16.1 = 148.12 mm^2
SA top = 2.79/2 (4+9.2) = 18.414 mm^2 used Pythagoras to get perpendicular height of trapezium h^2 = 5.9^2 - 5.2^2, h = 2.79
SA bottom = 18.414 mm^2
Total SA = 439.3 mm^2 (to one decimal place)
The actual answer says it is 512.0 mm^2 (to one decimal place)
Question 4
Find the volume of the following truncated shape
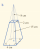
Volume of large pyramid = 1/3 (4 x 4) x 15 = 80 cm^3
Volume of small pyramid = 1/3 (2 x 2 ) x 8 = 32/3 cm^3
Volume of truncated shape = 80 - 32/3 = 69.3 cm^3
The actual answer is 112 cm^3
Question 5
Find the area of the shaded area correct to 1 decimal place

Area of entire sector = 1/6 x pi x 14^2
= 98/3 pi cm^2
Area of small sector = 1/6 x pi x 3^2
= 3/2 pi cm^2
Area of shaded region = 98/3 pi - 3/2 pi = 97.9 cm^2 (to one decimal place)
The actual answer is 39. 3 cm^2
Find the surface area (to one decimal place)

SA top = 1/2 x 9 x 12 = 54 cm^2
SA bottom = 1/2 x 9 x 12 = 54 cm^2
SA front = 1/2 x 12 x 5 = 30 cm^2
SA back = 1/2 x 15 x 5 = 37.5 cm^2 (used Pythagoras to get base of 15 cm)
Total SA= 175.5 cm^2
The actual answer says it is 180cm^2 (to one decimal place)
Question 2
Find the surface area (to one decimal place)

SA front = (1/2 x 20 x 6) + (20 x 15) = 360 cm^2
SA back = 360 cm^2
SA bottom = 30 x 20 = 600 cm^2
SA RHS = (30 x 15) + (11.66 x 30) used Pythagoras to find width of rectangle w^2 = 10^2 +6^2, w = 11.66 cm
= 799.86 cm^2
SA LHS = 799.86 cm^2
Total SA = 2919.7 cm^2 (to one decimal place)
The actual answer says it is 2819.2 cm^2 (to one decimal place)
Question 3
Find the surface area (to one decimal place)

SA RHS = 16.1 x 5.9 = 94.99 mm^2
SA LHS = 94.99 mm^2
SA front = 16.1 x 4 = 64.4 mm^2
SA back = 9.2 x 16.1 = 148.12 mm^2
SA top = 2.79/2 (4+9.2) = 18.414 mm^2 used Pythagoras to get perpendicular height of trapezium h^2 = 5.9^2 - 5.2^2, h = 2.79
SA bottom = 18.414 mm^2
Total SA = 439.3 mm^2 (to one decimal place)
The actual answer says it is 512.0 mm^2 (to one decimal place)
Question 4
Find the volume of the following truncated shape

Volume of large pyramid = 1/3 (4 x 4) x 15 = 80 cm^3
Volume of small pyramid = 1/3 (2 x 2 ) x 8 = 32/3 cm^3
Volume of truncated shape = 80 - 32/3 = 69.3 cm^3
The actual answer is 112 cm^3
Question 5
Find the area of the shaded area correct to 1 decimal place

Area of entire sector = 1/6 x pi x 14^2
= 98/3 pi cm^2
Area of small sector = 1/6 x pi x 3^2
= 3/2 pi cm^2
Area of shaded region = 98/3 pi - 3/2 pi = 97.9 cm^2 (to one decimal place)
The actual answer is 39. 3 cm^2


