Just not quite sure about how the answer is obtained in this question. Below is the question. Thanks
A man M walks along a pier, represented by the positive y-axis, pulling on a boat B(x,y) by a rope of length L. The man is initially at the origin O and the boat is initially on the x-axis, L metres from O, The man keeps the rope taut and the path followed by the boat is such that the rope is always tangent to the curve tracing its path.
i) let the path followed by the boat be the graph of the function y=f(x). By considering the gradient of the line MB, show that
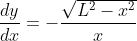
ii) The man walks along the pier such that the boat moves in the y-direction at a constant rate of 3m/s. Find the rate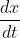 at which the boat approaches the pier, when it is a distance
at which the boat approaches the pier, when it is a distance 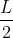 metres horizontally from the pier
metres horizontally from the pier
(the answer is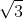 m/s)
m/s)
A man M walks along a pier, represented by the positive y-axis, pulling on a boat B(x,y) by a rope of length L. The man is initially at the origin O and the boat is initially on the x-axis, L metres from O, The man keeps the rope taut and the path followed by the boat is such that the rope is always tangent to the curve tracing its path.
i) let the path followed by the boat be the graph of the function y=f(x). By considering the gradient of the line MB, show that
ii) The man walks along the pier such that the boat moves in the y-direction at a constant rate of 3m/s. Find the rate
(the answer is

