For this one, you see that
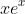
is two terms multiplied together right so thus you need to use the product rule to obtain
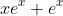
.
If you are integrating then you are going to notice a very important fact
=xe^{x}+e^{x})
-e^{x}dx)
Which then becomes
dx-\int_{0}^{2}e^{x}dx)
This is simply
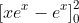
I reckon you can handle the rest and for part b use the same idea.