Exponential function (1 Viewer)

RoXaH · Jul 8, 2009

a)Calculate the area bounded by y=e^x, the coordinate axes and the tangent at x = 2
b) Calculate the area bounded by y=e^x, the Y axis and the line y=e^2

kurt.physics · Jul 8, 2009

RoXaH said:
a)Calculate the area bounded by y=e^x, the coordinate axes and the tangent at x = 2
b) Calculate the area bounded by y=e^x, the Y axis and the line y=e^2

(note: for these problems drawing a diagram is absolutely essential!)
Lets find the equation of the tangent at x = 2

$y = e^x$

$y' = e^x$

$$When$\,\,x =2, y = e^2\,\,$and$\,\,y' = e^2$

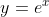
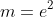
So the gradient of the tangent is $m = e^2$ and the tangent goes through the point $\left(2, e^2\right)$

So by the point gradient formula

$y - y_{1} = m\left(x - x_{1}\right)$

$y - e^2 = e^2\left(x - 2\right)$

$y = x \cdot e^2 - e^2$

To find the area enclosed between the tangent, the curve and the axes we find the area under the curve, ie y = e^x, then subtract the area under the tangent. So:

$\int_{0}^{2} e^x\, dx - \int_{1}^{2}\left(e^2 x - e^2\right) dx$

Note that we are taking the integral between 1 and 2 for the tangent because the tangent is below the x-axis between 0 and 1 and so that area would be negative (which we don't want). Proceeding,

$=\left[e^x\right]_{0}^{2} - \left[\frac{e^2x^2}{2} - e^2 x\right]_{1}^{2}$

$= \left[e^2 - e^0\right] - \left[\frac{e^2\cdot(2)^2}{2} - 2e^2 - \left(\frac{e^2\cdot (1)^2}{2} - e^2\right)\right]$

$= e^2 - 1 + \frac{e^2}{2} - e^2$

$= \boxed{\left(\frac{e^2}{2} - 1\right) units^2}$

(ii) Note that if we were to find the area bounded by the y-axis we would have to change y = e^x in terms of y instead of x, the result being x = log_e y. But you cannot integrate log_e y.

Use the graph you constructed in the last question. We know that y = e^2 when x=2. Draw both the lines y = e^2 and x = 2. Note that this forms a rectangle. We can find the area under the curve y = e^x between 0 and 2, then subtract that from the rectangles area which would give us the area bounded by the y-axis. So, the area under the curve y = e^x between x =0 and x = 2 is:

$\int_{0}^{2} e^x dx = \left[e^x\right]_{0}^{2}$

$= e^2 - e^0 = e^2 - 1$

The area of a rectangle is length times width, ie

$A_{rectangle} = 2e^2$

And so the area bounded by the y-axis is:

$A = 2e^2 - (e^2 - 1)$

$= 2e^2 - e^2 + 1$

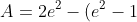$= \boxed{\left(e^2 + 1\right) units^2}$

Aquawhite · Jul 8, 2009

Great answer... just don't spend so long explaining in the HSC lol... but great to help others who ask the question to fully understand.

Exponential function (1 Viewer)

RoXaH

New Member

kurt.physics

Member

Aquawhite

Retiring

Users Who Are Viewing This Thread (Users: 0, Guests: 1)