namelyanonymous
Member
I can't seem to get this one:
Show that a^2 + b^2 + c^2 >= ab + bc + ca and hence show that:
b)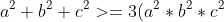^{1/3} )
I got the first part, its just (b) that I dont know how to work with :/ any hints greatly appreciated.
Show that a^2 + b^2 + c^2 >= ab + bc + ca and hence show that:
b)
I got the first part, its just (b) that I dont know how to work with :/ any hints greatly appreciated.

