With these sorts of questions it may help to remember your definitions and think things through slowly and methodically.
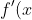 )
is the gradient function. That means that the value of
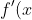 )
is the gradient of
 )
at
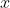
.
A gradient of 0 means that there is a stationary point.
As the gradient approaches zero, the graph approaches a horizontal line. If it approaches zero from the positive side, then you know that
 )
has a maximum there, because the gradient is always positive (i.e. the graph is going up) before it reaches zero and vice versa for the negative side.
A positive gradient means the graph is going up.
A negative gradient means the graph is going down.
As the gradient approaches infinity, the graph approaches a vertical line (whether it goes up or down depends on if its positive or negative infinity). This means a local maximum/minimum in the graph of
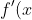 )
means the graph of
)
is (relatively) steepest at that point, because as
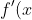 )
approaches its (local) maximum/minimum value, the graph of
 )
gets increasingly steeper.
A good way to visualise this is to look at graphs of a polynomial and its derivatives, and examine what happens to the polynomial when its derivative is approaching zero or approaching a local minimum/maximum.