Hey could someone please explain (iii)?
The total change of the function value from
x = 0 to
x = 4 is:
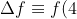 - f(0) = \int _0 ^4 f^\prime (x) \text{ d}x)
.
However, this integral is 0, as seen from the sketch.
So
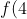 - f(0) = 0 \Rightarrow f(4) = f(0) = 0)
.
From
x = 4 to
x = 6, the rate of change of the function value is just a constant -3 (since
 = -3)
here), so the function is a straight line in this interval.
So the change in function value over this interval is:
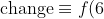 - f(4) = (\text{rate of change})\times (\text{change in }x)\Rightarrow f(6) =\text{starting value (i.e. } f(4))+(\text{rate of change})\times (\text{change in }x)= f(4) + (-3)(6 - 4) = 0 -3\times 2 = -6)
.

