You can get the upper bound for the first integral by solving
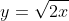
for
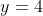
. Then evaluate the integral and subtract it from a rectangle to get your answer.
Alternatively, you can get the answer directly by switching
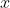
and
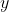
, rearranging to make

the subject and integrating from 0 to 4. The curve will become a parabola, but it doesn't affect the integral.
______________________________________________
The latus rectum of
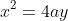
is
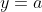
.
If you shift the parabola down by

, we can integrate on the x-axis (the areas will still be the same). To get the bounds, find the x-intercepts of the new shifted parabola. Finally, take the absolute value of the integral to get the area.

