-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Integration Partial Fractions Q (1 Viewer)
- Thread starter hmim
- Start date
Oh yeah, i figured out the first one, but I don't know how to do b and c specifically. Would you be able to shown one of them please?View attachment 38606
Heres a quick solution to the first one (which ig you can use to figure out the rest), you definitely don’t need long division though.
View attachment 38607
And how did they let LHS = RHS from in this case? Where did the A/x come from, and on the x^2 term, should it be Bx + c
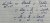
It’s just a bit of a shortcut, you still get there if you do it like normal
Thank you so much for all your help! It makes sense nowView attachment 38610
It’s just a bit of a shortcut, you still get there if you do it like normal
unofficiallyred12
Member
- Joined
- Aug 4, 2021
- Messages
- 85
- Gender
- Male
- HSC
- 2023
hmm interestingly b and c don't require partial fractions at all
no question really requires partial fractions, with the right algebraic manipulation you can always avoid ithmm interestingly b and c don't require partial fractions at all
unofficiallyred12
Member
- Joined
- Aug 4, 2021
- Messages
- 85
- Gender
- Male
- HSC
- 2023
I disagree there are certain qs that definitely require partial fractions it just so happens that when u have degree of numerator = denominator u can usually avoid itno question really requires partial fractions, with the right algebraic manipulation you can always avoid it
unofficiallyred12
Member
- Joined
- Aug 4, 2021
- Messages
- 85
- Gender
- Male
- HSC
- 2023
also there are qs like a in which u should be able to avoid partial fracs pre easily but the decomposition is so free u might as well just do it
howcanibesmarter
Well-Known Member
Hey, so I've noticed someone already gave you the solutions, but i just want to quickly add:View attachment 38605
Can someone please show their working for these types of partial fractions q's where the numerator has a higher degree than the numerator. I'm so lost and the Cambridge method isn't clear to me. Is there a faster way than long division?
The main rules for partial fractions (well ig they aren't actual rules but it sort of follows a structure)
TYPICALLY (not all cases but most)
--> If top and bottom powers are the same - U look at the coefficients. For example a) b) c) d) they all leave a constant of 1 out the front. This means you'll have one less term to find out. --> Less chance of errors.
--> There's an alternate method in finding the unknown A,B,C etc quickly. Its called "cover-up rule". Cambridge textbooks specifically used it, and it's a lot faster than equating coefficients or substitution. However to my knowledge it is only applicable when the denominator is something like (x-3)(x-2) (example d) etc. Generalising it such that it makes more sense ig would be distinct brackets that are single power. In this case, you can use it for a, b, and d just fine. (if you want i can send a worked solutions)
--> Whenever top power is greater than the bottom power - You really only have three choices. One, partial fractions. i.e. e) Your term out the from would be (Ax+B) + Whatever left. Two, you simply do a long division (typically the best choice, unless the powers are low and its a standard integral) That being said, three is algebraic manipulation. I would advise against this method, unless you've seen or done enough questions to get it quickly, otherwise i would just recommend to do a long divide.
When do you know you have to do partial in a test?
Well, firstly they might give you a part a), asking you to find out the fraction and unknowns itself. Simple, it's definitely partial.
Whenever the top power is less than the bottom power. --> Not always the case though, you have to see its not some log thing where its the diff on the top.
When the bottom can be factorised. Generally speaking, if bottom is factorisable, and top power is lower, you cant seem to work out any other method... its most likely partial.
Hope this clears it up a bit, because these questions should be easy marks to get in a test, you don't wanna be relying on inequalties cus those are yikes.
hmm how would you approach it then?hmm interestingly b and c don't require partial fractions at all
Thanks so much for this !!Hey, so I've noticed someone already gave you the solutions, but i just want to quickly add:
The main rules for partial fractions (well ig they aren't actual rules but it sort of follows a structure)
TYPICALLY (not all cases but most)
--> If top and bottom powers are the same - U look at the coefficients. For example a) b) c) d) they all leave a constant of 1 out the front. This means you'll have one less term to find out. --> Less chance of errors.
--> There's an alternate method in finding the unknown A,B,C etc quickly. Its called "cover-up rule". Cambridge textbooks specifically used it, and it's a lot faster than equating coefficients or substitution. However to my knowledge it is only applicable when the denominator is something like (x-3)(x-2) (example d) etc. Generalising it such that it makes more sense ig would be distinct brackets that are single power. In this case, you can use it for a, b, and d just fine. (if you want i can send a worked solutions)
--> Whenever top power is greater than the bottom power - You really only have three choices. One, partial fractions. i.e. e) Your term out the from would be (Ax+B) + Whatever left. Two, you simply do a long division (typically the best choice, unless the powers are low and its a standard integral) That being said, three is algebraic manipulation. I would advise against this method, unless you've seen or done enough questions to get it quickly, otherwise i would just recommend to do a long divide.
When do you know you have to do partial in a test?
Well, firstly they might give you a part a), asking you to find out the fraction and unknowns itself. Simple, it's definitely partial.
Whenever the top power is less than the bottom power. --> Not always the case though, you have to see its not some log thing where its the diff on the top.
When the bottom can be factorised. Generally speaking, if bottom is factorisable, and top power is lower, you cant seem to work out any other method... its most likely partial.
Hope this clears it up a bit, because these questions should be easy marks to get in a test, you don't wanna be relying on inequalties cus those are yikes.
howcanibesmarter
Well-Known Member
I wouldnt personally do it, but for this purpose ig you would just add one and minus one on the numerator. Hopefully you see that you get a difference of two squares, which u can cancel a (x-1) from the denominator. Splitting this fraction up SHOULD get you 1 +1/x +smthing else...U can go from there i think. Similar method would be applied to c). But again, would be quicker to just go straight to partial unless you are very confident with thinking in ur head.hmm how would you approach it then?
I could be wrong, so someone please correct me since i dont have paper w me
yeah you definitely could do it this way but I usually avoid it unless it’s a really simple question because it’s a lot easier to make mistakes doing that than partial fractionsI wouldnt personally do it, but for this purpose ig you would just add one and minus one on the numerator. Hopefully you see that you get a difference of two squares, which u can cancel a (x-1) from the denominator. Splitting this fraction up SHOULD get you 1 +1/x +smthing else...U can go from there i think. Similar method would be applied to c). But again, would be quicker to just go straight to partial unless you are very confident with thinking in ur head.
I could be wrong, so someone please correct me since i dont have paper w me
wait the smth else is still +2/(x^2-x) which u still need partial fractions forI wouldnt personally do it, but for this purpose ig you would just add one and minus one on the numerator. Hopefully you see that you get a difference of two squares, which u can cancel a (x-1) from the denominator. Splitting this fraction up SHOULD get you 1 +1/x +smthing else...U can go from there i think. Similar method would be applied to c). But again, would be quicker to just go straight to partial unless you are very confident with thinking in ur head.
I could be wrong, so someone please correct me since i dont have paper w me
I’d call that one more algebraic manipulations than partial fractions (I may be wrong but that’s how I’d do a question like that). When ur doing questions like that with high numerator degrees, your main goal should be to try to reduce the numerator degrees until they’re more manageable. For example, for this question without part a, you’d add a second integral so that you could make the first integral numerator a multiple of the denominator to get rid of the x^2 (hence the a) and then make the second one into a multiple of x-2 to cancel out all of the x, and then lastly you just have a simple constant on the numerator for an easy reverse chain rule.View attachment 38616
What about this one, what's the process for determining partial fractions when the degree of the numerator is greater than or equal to denominator. Where did this A come from?
Hopefully that makes sense, if not I can write up some working if you’d like
unofficiallyred12
Member
- Joined
- Aug 4, 2021
- Messages
- 85
- Gender
- Male
- HSC
- 2023
u can -2x + 2x on the numerator instead, then u get (x-1)/x + 2x/(x^2-x) which is a very simple integral. for c tho u can literally split it up then evaluate integral of 1/(x^3+x) by dividing both sides by x^3 and doing reverse chain rule. +-x^2 on the numerator also works pre nicely. d, you can also bypass partial fractions but this time using a u sub but i think the usual method would be faster in exam circumstances so u'd prolly stick with thatwait the smth else is still +2/(x^2-x) which u still need partial fractions for







