I'm pretty sure spherical coordinates are not required... cylindrical coordinates make the problem much nicer, but they're not required to solve the problem "conceptually". Anyway you can do it also like, by using spherical coordinates but in terms of like, cones etc. Not too hard, no integration of the coordinates required.
We note that whether or not the point is a solution
depends only on its latitude, since the problem is invariant/symmetrical upon rotation about the planets axis - this follows from the definition of north/south/east/west being the directions up/down along the axis for N/S, and perpendicular to the axis for E/W. Now note because of this as well, if you move north 1km, move any amount E/W, then move down 1km, you will always arrive back at the original latitude/z-coordinate. Thats coz moving E/W is equivalent to rotating the planet, and latitude is invariant under that. so all you require is that the longitude before/after moving 1km east/west is the same. Now note that, the change in longitude when moving 1km east/west is directly proportional to the radius of the circle defined by all points of that same latitude (from definition of radians/angles), and the radius of that circle is given by
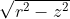
, where r is the radius of the whole planet and z is the z-coordinate corresponding to that latitude (when taken in cylindrical coordinates). From this its obvious after moving 1km north, the absolute value of the z-coordinate has to be the same; i.e. it has to move 1km north to the reflection of that latitude about the equator. I.e. all such points lie on the circle of latitude thats distance 0.5 km from the equator; if you take the radius of the planet to be 1000km, that gives all points of latitude 1/2000 or -1/2000 radians or +/- 9pi/100 degrees.


