-
Best of luck to the class of 2024 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Locus of complek numbers (1 Viewer)
- Thread starter Aysce
- Start date
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
There will be two cases, depending on the value of k:
From the original expression, we acquire the quadratic:

Using the quadratic formula, we have:

Remember that z is a complex number, so it can be real or complex (since the field of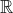 is a subfield of
is a subfield of 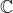 )
)
Hence, we can have 3 cases for the inside of the square root. It can be positive or equal to zero (real) or less than zero (complex):
For the real case:

This implies that:

Hence, the locus if z is real is y=0 or in other words, the x axis.
Now consider the unreal case:


But since the inside of the square root is negative, we will re-write it this way (it's the same thing if you expand the i back inside):

We will now separate them so we can have a very obvious real and unreal component:


Equate the real and unreal components:


We now make k^2 the subject, using the expression we acquired by equating real:

Substitute it back into the expression we had for y (so we are basically eliminating k):

With a bit of manipulation, which will involve squaring both sides, we acquire the expression:

And this is the locus for the unreal case, which is acquired when:

So to finalise our answer, our two possible loci are either the x axis, or the unit circle.
From the original expression, we acquire the quadratic:
Using the quadratic formula, we have:
Remember that z is a complex number, so it can be real or complex (since the field of
Hence, we can have 3 cases for the inside of the square root. It can be positive or equal to zero (real) or less than zero (complex):
For the real case:
This implies that:
Hence, the locus if z is real is y=0 or in other words, the x axis.
Now consider the unreal case:
But since the inside of the square root is negative, we will re-write it this way (it's the same thing if you expand the i back inside):
We will now separate them so we can have a very obvious real and unreal component:
Equate the real and unreal components:
We now make k^2 the subject, using the expression we acquired by equating real:
Substitute it back into the expression we had for y (so we are basically eliminating k):
With a bit of manipulation, which will involve squaring both sides, we acquire the expression:
And this is the locus for the unreal case, which is acquired when:
So to finalise our answer, our two possible loci are either the x axis, or the unit circle.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
^^^ pokka's method is very good. It gives you the locus faster than my method, but I'm not sure how it would determine the range of k such that we would use y=0 or the unit circle.
Also might I add a correction to my solution. Where it says:

It should say:

Also might I add a correction to my solution. Where it says:
It should say:
largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 202
- Gender
- Male
- HSC
- 2011
Ive got another way which I think is much faster, using real/imaginary parts and modulus/argument and de moivres:In pokka's method a faster way would be from line two and:
View attachment 24289
And thus if z+1/z is real, it has imaginary part zero, so either
The first case gives the entire x axis (with the origin removed of course since there 1/z isnt defined), the second gives r = 1 (as r is a positive real) i.e. the unit circle.
Basically Ive done it geometrically. To go from z to 1/z, you reflect it about the x-axis and then change its modulus to the inverse of its modulus. If z+1/z = 0 then, the "height" of z above the x-axis is going to be equal to the "height" of 1/z BELOW the x-axis, and its very easy to see that only happens if the modulus of z and the modulus of 1/z are the same i.e. if z is on the unit circle.
Aysce
Well-Known Member
- Joined
- Jun 24, 2011
- Messages
- 2,394
- Gender
- Male
- HSC
- 2012
Very nice methods but one question, how do you know which one to take as the locus?
I also have another question if you guys don't mind.
Q. If R is a real number, find the locus of z defined by z = (1+iR)/(1-iR)
Now I multiplied by the conjugate and let z = x+iy where I then equated real and imaginary coefficients. Based on Terry Lee's solution, (Page 52 Q8) it automatically uses x^2 + y^2 when you gain x and y to find the locus. Why do they do this? I don't understand why he did this.
I also have another question if you guys don't mind.
Q. If R is a real number, find the locus of z defined by z = (1+iR)/(1-iR)
Now I multiplied by the conjugate and let z = x+iy where I then equated real and imaginary coefficients. Based on Terry Lee's solution, (Page 52 Q8) it automatically uses x^2 + y^2 when you gain x and y to find the locus. Why do they do this? I don't understand why he did this.


