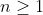First step for the first one
Q for reference
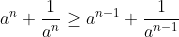
for all positive integers
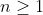
. Where
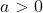
First step for n=1
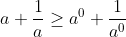
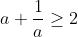
The assumption step which is
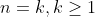
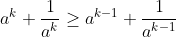
There we are RTP for
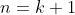
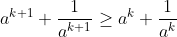
Using assumption
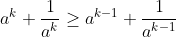
times both sides by a and there we will have
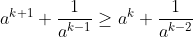
Add
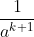
and take
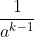
on both sides
Performing these steps. We will have.
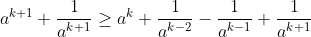
We want
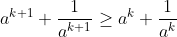
.
But of course this is where it gets fun
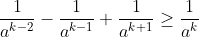
. A vital step to prove that
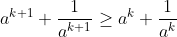
because if that is true then you have finished the induction proof. I imagine this would be the trickiest step.
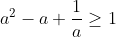
multiplying by
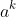
on both sides because from the Q
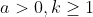
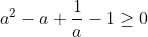
.
At this point you go, uh what do I do nor do I have anything to offer.
Well, if in doubt this is when we will use calculus.
Differentiate with respect to a
)
Now you want to find stationary points,
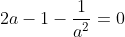
Multiply by
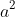
It becomes
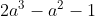
\left(2a^{2}+a+1\right))
a=1 because the other solution is imaginary
Differentiate that again we will receive
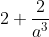
sub in
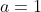
. We will have 4 which clearly is greater than 0 so therefore we have a minimum point. Therefore, we have just proven that
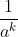
is the minimum value and using
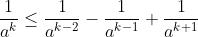
the indicution proof of
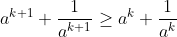
is complete for