Note that the two curves given are inverse functions, and thus reflections in
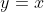
.
The points
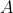
and
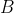
lie on
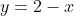
, which is perpendicular to
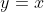
.
Consider
)
, which is also on
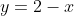
but further from
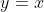
than is
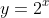
because
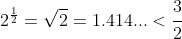
.
The reflection of
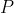
in
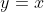
is
)
.
The distance
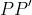
is greater than the distance
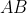
as
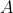
and
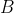
lie between
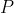
and
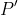
on
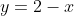
.
Further, the distance
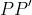
is
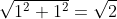
.
Thus the distance
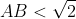
, as required.