Hey guys,
Two questions,
Q: Find the sum of: 1 - 2 + 3 - 4 + 5 -6 + ... - 100
Q: What is the least number of terms required if the sum of 15 + 20 + 25 +... is to exceed 2625?
Thanks in advance!
First one:
We cannot deal with that series as a whole, so its best to split it into 2 separate ones:
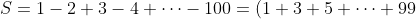 - (2 + 4 + \dots + 100) )
Each of them are arithmetic series each with a common difference of 2 (but different initial term). So using the sum formula:
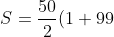 - \frac{50}{2}(2+100) = 25 \times 100 - 25\times 102 = -50)
Second one:
We will denote a general term:
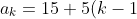 )
We need to find the lowest k required so that:

Sum the LHS using the sum formula:
 \times 5 ) > 2625 )
 > 2625 )


Now we simply have to solve it.

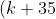(k-30) > 0 )
(using the quadratic formula I found the 'roots')
And since k must be positive:

That means the lowest value of k, or the least number of terms required is 31. (not 30 as that equals 2625).