There's this question that I dunno how to tackle :|
A person throws a cricket ball so that it's path is given by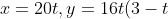) , where
, where  and
and  are measured in metres and
are measured in metres and 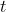 in seconds. Find the:
in seconds. Find the:
a) Initial velocity and the initial angle of projection.
b) Find the greatest height reached.
c) Find the distance which the ball covered.
This was from MathsInFocus Extension 1 textbook, and it gives answers, but not working.
Could someone show me the working please?
(After I know how to work out part a), I can do the rest )
)
A person throws a cricket ball so that it's path is given by
a) Initial velocity and the initial angle of projection.
b) Find the greatest height reached.
c) Find the distance which the ball covered.
This was from MathsInFocus Extension 1 textbook, and it gives answers, but not working.
Could someone show me the working please?
(After I know how to work out part a), I can do the rest
