-
Looking for HSC notes and resources? Check out our Notes & Resources page
Complex (2 Viewers)
- Thread starter nrlwinner
- Start date
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
this is a nice Q
Last edited:
Yeah thanks, but how would you know you had to add.
this is a nice Q
I tried doing it by subing into the equation, trying to prove LHS=RHS
I got up to.
LHS =
But cant seem to get it to equal z1z2
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
gurmies
Drover
This is a nice solution.
this is a nice Q
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
Ok. I tried taking modulus and I realised I couldn't get it.
The question was.
If
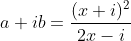
Prove
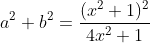
Man, are you a genius?
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
Last edited:
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
=$Man, are you a genius?
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
I'm stuck on another question

I've proved that if
then it's an equilateral triangle.
But I need help to show
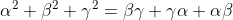
Last edited:
gurmies
Drover
You've posted this question already...although this disguises it quite nicely.I'm stuck on another question

I've proved that if
then it's an equilateral triangle.
But I need help to show
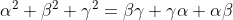
Can someone start me off, because I've got no clue what to do, but not finish it. I wanna have a go.
Also need help with the last question of my paper, and then I'm done!!! I've tried employing the strategies you guys showed me in the previous questions, but this one puts me off because there are 3 brackets, and the vectors are reversed.
z1,z2,z3 are represented by the points p1,p2,p3 respectively. If p1p2p3 is an equilateral triangle, show
Last edited:
I worked out a way to do your first question, but I don't know how to describe it in part. The only clue I can give is that at starts out as a circle geometric proof, and by playing with Arguments, turns algebraic. Tell me if you want to see it.
Yeah, I was on that track but didn't think it was right. May I see the solution?
Well, I don't know how to draw a diagram here, so I'll have to describe it for you.
Draw your circle through O, predominantly in the first quadrant. Let A, B, C represent z1, z2, z3 respectively. For ease of describing, draw O, A, B, C in clockwise order (and in left to right order), all in the first quadrant. (The same logic works if they are drawn otherwise.) Produce AB to D.
Angle AOC = arg z1 - arg z3.
Angle CBD = arg (z1 - z2) - arg (z2 - z3)
(Tell me if you don't get that)
So arg (z1 - z2) - arg (z2 - z3) = arg z1 - arg z2 [ext angle of cyclic quad = opp int angle]
Rearrange:
arg(z1 - z2) - arg z1 = arg (z2 - z3) - arg z3
Add in the same 'fudge factor' on both sides of the =:
arg (z1 - z2) - arg z1 - arg z2 = arg (z2 - z3) - arg z3 - arg z2
Can you see that it is now proved?
What's D?
