-
Best of luck to the class of 2024 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Preliminary mathematics marathon (1 Viewer)
- Thread starter ohexploitable
- Start date
hscishard
Active Member
I went (cos2x)^2/2 = cos2xsplit cos^2x 2x into cos 2x . cos2x
product rule
did anyone do it another way?
hscishard
Active Member
LHS=cos(3x)Prove that:
cos 3 theta = 4cos^3theta- 3 cos theta
= cos(2x + x)=cos2x(cosx) - sin2x(sinx)
=(2cos^2(x) -1)(cosx) - 2sinxcosx(sinx)
=2cos^3x - cosx - 2sin^2x(cosx)
=2cos^3(x) - cosx -2(1-cos^2x)cosx
=2cos^3(x) - cosx -2cosx +2cos^3x
=4cos^3(x) -3cosx = RHS
Pain to type man
Entrant
Banned
- Joined
- May 20, 2010
- Messages
- 147
- Gender
- Male
- HSC
- 2011
Re: another question
taking derivatives of both sides
(2x+2ydy/dx)(x^2+y^2)2 = 2(2ydy/dx+2x)
(2x+2ydy/dx)(x^2+y^2)=(2ydy/dx+2x)






2x^3+2x^2ydy/dx+2y^3dy/dx+2xy^2dy/dx = 2ydy/dx+2x
moving everything with dy/dx onto one side.
2x^3-2x=2ydy/dx-2x^2ydy/dx-2y^3dy/dx-2xy^2dy/dx
2x(x^2-1)=[dy/dx](2y-2x^2y-2y^3-2xy^2)
therefore
dy/dx = 2x(x^2-1)/(2y-2yx^2-2y^3-2xy^2
= 2x(x^2-1)/[2y](1-x^2)-2y^2(y-2x)
think i got it wrong. but you try doing it on a computer.
I broke my scanner ages ago.
Hint for those attempting it: Use implicit differentiation. Although I think this is in HSC course, not prelim anyway.
New Question:
Lemniscate of Bernoulli - Wikipedia, the free encyclopedia
(x^2 + y^2)^2 = 2(y^2+x^2)Hint for those attempting it: Use implicit differentiation. Although I think this is in HSC course, not prelim anyway.
taking derivatives of both sides
(2x+2ydy/dx)(x^2+y^2)2 = 2(2ydy/dx+2x)
(2x+2ydy/dx)(x^2+y^2)=(2ydy/dx+2x)
2x^3+2x^2ydy/dx+2y^3dy/dx+2xy^2dy/dx = 2ydy/dx+2x
moving everything with dy/dx onto one side.
2x^3-2x=2ydy/dx-2x^2ydy/dx-2y^3dy/dx-2xy^2dy/dx
2x(x^2-1)=[dy/dx](2y-2x^2y-2y^3-2xy^2)
therefore
dy/dx = 2x(x^2-1)/(2y-2yx^2-2y^3-2xy^2
= 2x(x^2-1)/[2y](1-x^2)-2y^2(y-2x)
think i got it wrong. but you try doing it on a computer.
I broke my scanner ages ago.
Re: another question


i likeI went (cos2x)^2/2 = cos2x
i dont like(x^2 + y^2)^2 = 2(y^2+x^2)
taking derivatives of both sides
(2x+2ydy/dx)(x^2+y^2)2 = 2(2ydy/dx+2x)
(2x+2ydy/dx)(x^2+y^2)=(2ydy/dx+2x)
2x^3+2x^2ydy/dx+2y^3dy/dx+2xy^2dy/dx = 2ydy/dx+2x
moving everything with dy/dx onto one side.
2x^3-2x=2ydy/dx-2x^2ydy/dx-2y^3dy/dx-2xy^2dy/dx
2x(x^2-1)=[dy/dx](2y-2x^2y-2y^3-2xy^2)
therefore
dy/dx = 2x(x^2-1)/(2y-2yx^2-2y^3-2xy^2
= 2x(x^2-1)/[2y](1-x^2)-2y^2(y-2x)
think i got it wrong. but you try doing it on a computer.
I broke my scanner ages ago.
Entrant
Banned
- Joined
- May 20, 2010
- Messages
- 147
- Gender
- Male
- HSC
- 2011
Re: another question
its wrong i know, but i cbf fixing it.
find for values of x which
x^-1+x^2/2-x^-3/3+x^4/4-x^-5/5...-x^-(n-1)/n-1+x^n/n = 0.999
IF n IS AN EVEN NUMBER.
its wrong i know, but i cbf fixing it.
find for values of x which
x^-1+x^2/2-x^-3/3+x^4/4-x^-5/5...-x^-(n-1)/n-1+x^n/n = 0.999
IF n IS AN EVEN NUMBER.
Last edited:
jeshxcore
Premium Member :)
Re: another question
(x^2 + y^2)^2 = 2(x^2 - y^2)
DIFFERENTIATE IMPLICITLY
2(x^2 + y^2)(2x + 2y.dy/dx) = 2(2x - 2y.dy/dx)
CANCEL OUT THE 2's AND EXPAND
(2x^3 + 2x.y.dy/dx + 2x.y^2 + 2y^3.dy/dx) = 2x - 2y.dy/dx
CANCEL OUT THE 2's AGAIN
x^3 + x.y.dy/dx + x.y^2 + y^3.dy/dx = x - y.dy.dx
dy/dx (x.y + y^3 + y) = x - x^3 - x.y^2
dy/dx = x(1 - x^3 - y^2)/y(x + y^2 + 1)
hopefully.. lol
(x^2 + y^2)^2 = 2(x^2 - y^2)
DIFFERENTIATE IMPLICITLY
2(x^2 + y^2)(2x + 2y.dy/dx) = 2(2x - 2y.dy/dx)
CANCEL OUT THE 2's AND EXPAND
(2x^3 + 2x.y.dy/dx + 2x.y^2 + 2y^3.dy/dx) = 2x - 2y.dy/dx
CANCEL OUT THE 2's AGAIN
x^3 + x.y.dy/dx + x.y^2 + y^3.dy/dx = x - y.dy.dx
dy/dx (x.y + y^3 + y) = x - x^3 - x.y^2
dy/dx = x(1 - x^3 - y^2)/y(x + y^2 + 1)
hopefully.. lol
jeshxcore
Premium Member :)
Re: another question
latex too much effort for me -.-
latex too much effort for me -.-
hscishard
Active Member
Re: another question
2(cosx-sinx)(cosx+sinx)= cosx -sinx
2(cosx+sinx)=1
sinx+cosx=1/2
Transforming:
R = root(1+1) = root 2
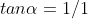
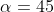
=1/2)
=\frac{1}{2\sqrt{2}})
204.3 and 335.7 1 d.p
First few steps aren't really that familiar..
Is there another way to do this?
2(cos^2-sin^2) = cosx - sinx2cos2x = cosx - sinx
solve for 0<=x<=360
2(cosx-sinx)(cosx+sinx)= cosx -sinx
2(cosx+sinx)=1
sinx+cosx=1/2
Transforming:
R = root(1+1) = root 2
204.3 and 335.7 1 d.p
First few steps aren't really that familiar..
Is there another way to do this?
jeshxcore
Premium Member :)
Re: another question
you cant "cancel out" cosx - sinx from both sides, that would result in you losing solutions2(cos^2-sin^2) = cosx - sinx
2(cosx-sinx)(cosx+sinx)= cosx -sinx
2(cosx+sinx)=1
sinx+cosx=1/2
Transforming:
R = root(1+1) = root 2
204.3 and 335.7 1 d.p
First few steps aren't really that familiar..
Is there another way to do this?
hscishard
Active Member
Transforming is gay. Bloody took out the quadratic.
hscishard
Active Member
Re: another question
Lol yea. It really did look better than doing the whole t forumla.you cant "cancel out" cosx - sinx from both sides, that would result in you losing solutions
Re: another question
Is your equation correct?its wrong i know, but i cbf fixing it.
find for values of x which
x^-1+x^2/2-x^-3/3+x^4/4-x^-5/5...-x^-(n-1)/n-1+x^n/n = 0.999
IF n IS AN EVEN NUMBER.
How can a square root be negative?
hscishard
Active Member
Can't you do this?If, then find the value of dy/dx when
.
y=(cos2x)^2/2 = cos2x
y'=-2sin2x
f'(pi/4)= -2sin(pi/2)
=-2
Oh btw, the -2 means a negative gradient. You prob didn't read the question correctly.
Last edited:
That's not entirely correct ...Can't you do this?
y=(cos2x)^2/2 = cos2x
Yes this is a red herring thus why I asked it.
Last edited:

