hscishard
Active Member
x^2 -1
You're askingh for the general one, arent you?
You're askingh for the general one, arent you?
yesx^2 -1
You're askingh for the general one, arent you?
What terms should be in there?
i know it's easy for u guys...
but i still don't know how to solve it by multiplying the square of the denominator.
greatly appreciated if someone can help
mmm hsc 2012, looking to get a head start?
First step: exclude values where denominator=0 { however, you will see this only matters when you have a "less than or equal" or a "greater than or equal"}
(2x+5)(x+1)^2 / (x+1) < 3(x+1)^2 { DONT EXPAND, it is easier to move all terms to one side and factorise, saves time}
(2x+5)(x+1)-3(x+1)^2 <0
(x+1) { (2x+5) -3(x+1) } <0
(x+1)( 2-x) <0
x<-1, x > 2 ( if you need explaination from the previous step to this one please ask)
thank you so much
shat brix
For some reason, I don't think that's correct
New Question:
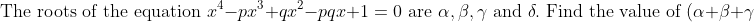(\alpha+\beta+\delta)(\beta+\gamma+\delta)(\alpha+\gamma+\delta))
The trick is to find a shortcut, it can be done in a few lines.thats not hard, just long, get some interesting questions lol
The trick is to find a shortcut, it can be done in a few lines.
lol what expand ( p -a) ( p-b) (p-c) ( p-d), where a, b, c, d are roots
its a little less work i guess
I felt special because I was the only one in class who thought of that.
