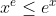y=ln x, dy/dx= 1/x
as the tangent passes through the origin, the tangent has an equation in the form
y=mx. But m=dy/dx,
. ' . solving simultaneously
ln x=1/x * x
ln x=1
x=e
when x=e, y=1
using (e,1) , m=1/e
y=x/e
I was wondering if a proof such as this is valid:
x^e is less than or equal to e^x
when x^e = e^x,
by inspection, x=e
when x approaches positive infinity, e^x>x^e
when x approaches 0, e^x>x^e
hence x^e is less than or equal to e^x?
it is true for x=0
then f(x) = e^(x) -> f ' (x) = e^(x)
g(x) = x^e -> g ' (x) = e x^(e-1)
now we need to show that f ' (x) > g ' (x)
f ' (x) / g ' (x) = [ e^(x) / [e x^(e-1) ] = e^(x-1) / x^(e-1) which is positive for all positive x ( x not equal to zero off course )
so f '(x) > g'(x)
hmm not 100% sure on the last step how we got x not equal to zero, but the statement is true for x=0
but kinda like that
EDIT: lol I think I know why, it is because they ( f(x) and g(x) ) are equal at x=0, and g' (0) =0 , we cannot divide by zero , such a dummy lol
EDIT: ahh not quite, need to show that the ratio is greater than one, that shouldnt be too hard, have just went round in a circle and reduced the powers by one, disregard this post