hscishard
Active Member
Determine the real values of gamma for which the equation defines an ellipse (terry lee 5.1 q7)
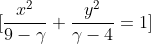
I got 4 < gamma < 6.5
Worked solution:
9-#>0
#<9
#-4>0
#>4
Therefore 4<#<9
The way the book did it doesn't seem right...
I got 4 < gamma < 6.5
Worked solution:
9-#>0
#<9
#-4>0
#>4
Therefore 4<#<9
The way the book did it doesn't seem right...

