UnrealAnchovies
Member
- Joined
- Apr 3, 2010
- Messages
- 777
- Gender
- Male
- HSC
- 2011
Haha yewwwwOMFG That's the book we use for 4u at my school! Just sayin'
I havent actually opened it yet though lol
Shit... How's the multiplicity stuff? I have to do that tomorrow night :/Haha yewwww
I went sweet in my first 4 unit assessment for the year, then did the summary exersise for the topic out of that textbook and mmmm... Struggle is the word that comes to mind.
Worried now hahah
Multiplication is easy peasy, it gets a bit harder when you're multiplying by double digits though :SShit... How's the multiplicity stuff? I have to do that tomorrow night :/
You seriously just made me like rofl. like fuckin' shit.Multiplication is easy peasy, it gets a bit harder when you're multiplying by double digits though :S
There was some good stuff in the "Hardest general maths topic?" thread but it doesn't work anymore.You seriously just made me like rofl. like fuckin' shit.
That's the best! LOL
I need to spread rep before giving you more
:-(There was some good stuff in the "Hardest general maths topic?" thread but it doesn't work anymore.
I was gonna answer this, but then I thought whether anyone has seen me do maths on here before. I don't think they have. I don't want to ruin it now.Hmm... lets get another question going...
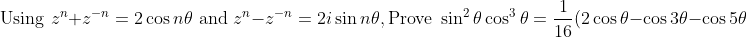)
If I was bothered I would, however I loathe questions like that D:Hmm... lets get another question going...
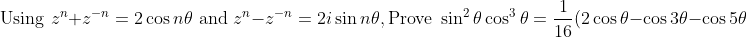)
thats just tons of algebraic manipulation(i) If [maths]P(x)=3x^4-11x^3+14x^2-11x+3[/maths] show that
[maths]P(x)=x^2(3(x+\frac{1}{x})^2-11(x+\frac{1}{x})+8)[/maths]
(ii) Hence solve P(x)=0 over C.
(i) If [maths]P(x)=3x^4-11x^3+14x^2-11x+3[/maths] show that
[maths]P(x)=x^2(3(x+\frac{1}{x})^2-11(x+\frac{1}{x})+8)[/maths]
(ii) Hence solve P(x)=0 over C.
x=0 is not a solution (sub into original equation to see)
If 0 isn't a solution he has 4x=0 is not a solution (sub into original equation to see)
and you have 5 solutions for degree 4 polynomial??
