Skeptyks
Member
- Joined
- May 6, 2011
- Messages
- 394
- Gender
- Male
- HSC
- 2012
Hey, just posted a thread but that was mathematics not maths ext 1 so I thought making a new thread would be appropriate.
In the figure, two tangents are drawn from the point) to the curve
to the curve 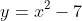 . Find the equations of the two tangents. (Note that the point lies outside the curve)
. Find the equations of the two tangents. (Note that the point lies outside the curve)
Now, I have let the gradient of the tangent to be known as
The equation of the tangent is therefore, .
.
Expanding it out,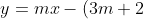) .
.
Now I have the equations:
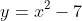
and
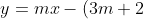)
So,
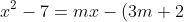)
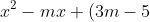=0)
Now, I am having a bit of trouble finding m...
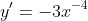
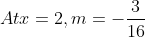
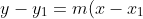)
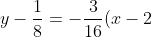)
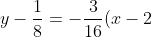)
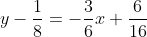
Now, we multiply both sides by 16.
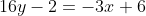
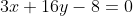
In the figure, two tangents are drawn from the point
Now, I have let the gradient of the tangent to be known as
The equation of the tangent is therefore,
Expanding it out,
Now I have the equations:
and
So,
Now, I am having a bit of trouble finding m...
Now, we multiply both sides by 16.
Last edited:
