Locus HELP (1 Viewer)
- Thread starter epicFAILx
- Start date
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
THE LOCUSAfter missing one lesson of tutoring i am now completely lost.
Can someone please explain to me what a locus is and what its used for!
Example 1.
The locus, no it is not an insect. Basically you are given some conditions. For example,
A point
The locus is the path or equation a point can take that satisfies the condition set.
In this case, the answer is
See how its perpendicular distance is always 3 units from the
So the locus is just an equation that satisfies a specific set of conditions/path.
Try these:
1. Find the locus of a point (x, y) that is always 6 units from the y axis.
2. Find the locus of a point (x, y) that is always 4 units from the x axis.
Example 2.
If we were given some harder questions such as,
Find the locus of a point that moves in a plane such that
Woah! What?
Let's us comprehend this "seemingly tricky" phrase. It's basically asking for the path which P can travel such that as it travels, the distance
First of all we need to find the distance of
Use the formula,
Now, let's find the distance
We must now equate them. Since they are the same distance from
Spiral tip: Draw these equations out for all of your graphs, including your locus! You will see what is happening.
Try these:
Find the locus of a point P(x, y) in a plane such that PA = PB:
1. If A = (-2, 3), B = (4, 5)
2. If A = (1, 7), B = (4, -2)
3.
EDITING
Last edited:
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Okay, I shall write a paragraph about that.Ahh, K.
Cool Thanks
But my main problem is with Parabolas. I mean stuff like: vertex, focus, directrix and axis of symettry
Last edited:
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
THE ANATOMY OF A PARABOLA
http://upload.wikimedia.org/wikipedia/commons/6/66/Parts_of_a_Parabola.JPG
Now. During Year 10 Mathematics when you are a baby your teacher told you there were three parts to a parabola right? The x intercept(s), the y intercept, the vertex and that was it. Now in Year 11 we can extend the definition of the parabola, we give it three more main parts, the focus, the directrix and the latus rectum.
Now you are use to the parabola as a smiley face and a sad face. We can extend the shape of the parabola into two more shapes, the sideways parabola. Kind of like a normal parabola but rotated to the left or right.
Okay back to business!
Your parabola equation can be written in two forms, the general equation form and the vertex form.
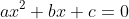 [Where
[Where  ]
]
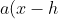^2 + k) [Where
[Where 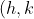) is our vertex and
is our vertex and  ]
]
Mr parabola is very cruel now days. They now expect you to learn the basic form of,
TYPE 1: NORMAL CONCAVE UP PARABOLA.
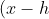^2 =4a(y-k))
Again we got (h, k) as our vertex.
But we got some new visitors! Mr Focal length, Mr Directrix. Better not confuse you, it's called the focal length and the directrix.
The focal length is and the directrix is I will illustrate this.
and the directrix is I will illustrate this.
I won't introduced the latus rectum just yet.
Now the only way we can comprehend this is to practice.
Example 1.
In the parabola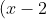^2=16(y+3)) . Find:
. Find:
a. The vertex: Easy, this can be read off it's)
b. The focus: This is also easy. Recall the form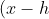^2 =4a(y-k)) and notice that our equation resembles that form.
and notice that our equation resembles that form.
Match everything up. We need to find . Since that is our focal length.
. Since that is our focal length.

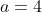
THAT'S OUR LENGTH, NOT OUR FOCUS POINT!
The focus if you looked at the picture, it's above the vertex. In this case, the focal length was 4 units. It is 4 units above the vertex. Draw the vertex of (2, -3)
We can see the focus is 4 units above it. Hence (2, 1) is the focus point.
c. The directrix was
So the directrix is below the vertex. It maintains 4 units below the vertex. Hence the directrix is (2, -7). However the directrix is an equation of the line.
So
TYPE 2: NORMAL CONCAVE DOWN PARABOLA.
It is in the form of,
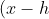^2=-4a(y-k))
Example 2.
In the parabola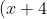^2=-16(y+3)) . Find:
. Find:
a. The vertex: Read off, (-4, -3).
b. The focus: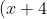^2=-16(y+3)) is identical to
is identical to 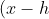^2=-4a(y-k)) .
.
So the focal is,

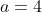 [Since it is the focal length.]
[Since it is the focal length.]
Now,
Our vertex (-4, -3). So, 4 below (Since focus is inside parabola and it is concave down.) is the focus.
Our focus is (-4, -7).
c. The directrix: 4 places above your parabola. It's the line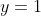
TYPE 3: SIDEWAYS PARABOLA SMILING TO THE RIGHT.
It is in the form of,
^2=4a(x-h))
Let's see an example.
Example 3.
Can you imagine me smiling to the right of the page? Oh wait. I don't smile. Anyway this parabola is sideways to the right.
If the parabola has an equation of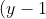^2=2(x+\frac{5}{2})) . Find the:
. Find the:
a. Vertex: Read off again! This time be careful. It's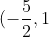)
b. Focus: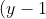^2=2(x+\frac{5}{2})) is identical to the form
is identical to the form ^2=4a(x-h))
The focus is

So if we grab our vertex again
It's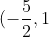) , the focus is inside the heart of the parabola. So we can see the heart of the parabola is to the right. If we go two places to the right,
, the focus is inside the heart of the parabola. So we can see the heart of the parabola is to the right. If we go two places to the right,
We get that the focus is)
c. Directrix: The directrix is outside the parabola. The focal length is So two spaces to the left,
So two spaces to the left, 
TYPE 4: SIDEWAYS PARABOLA SMILING TO THE LEFT.
It is in the form of,
^2=-4a(x-h))
Example 4.
If the parabola has an equation of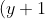^2=-2(x+2)) . Find the:
. Find the:
a. Vertex: Read off again, be careful. It's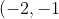)
b. Focus: We can see that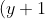^2=-2(x+2)) is identical to
is identical to ^2=-4a(x-h))
So
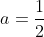 [Since lengths cannot be negative.]
[Since lengths cannot be negative.]
Our vertex was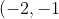) . The focus is in the heart of the parabola. Which is to the left. So
. The focus is in the heart of the parabola. Which is to the left. So  units to the left of
units to the left of 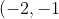) . That is,
. That is,
)
c. Directrix: Outside the heart of the parabola, so to the right. Hence it is
to the right. Hence it is 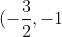) . But directrix is an equation. Hence it's
. But directrix is an equation. Hence it's 
Try these:
State the vertex, focus and directrix in these equations and draw the parabola out.
1.^2=4(y+2))
2.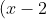^2 = -4(y+2))
3.^2 = 4(x+1))
4.^2 = -4(x+3))
Enough rambling. Feel free to ask me any questions and I will see if I can help you with understanding the latus rectum.
EDITING: Sorry for being slow, watching Disney's Enchanted.
[Note: Someone should check my working. It's after 9 pm, the time Spiral makes the most mistakes.]
http://upload.wikimedia.org/wikipedia/commons/6/66/Parts_of_a_Parabola.JPG
Now. During Year 10 Mathematics when you are a baby your teacher told you there were three parts to a parabola right? The x intercept(s), the y intercept, the vertex and that was it. Now in Year 11 we can extend the definition of the parabola, we give it three more main parts, the focus, the directrix and the latus rectum.
Now you are use to the parabola as a smiley face and a sad face. We can extend the shape of the parabola into two more shapes, the sideways parabola. Kind of like a normal parabola but rotated to the left or right.
Okay back to business!
Your parabola equation can be written in two forms, the general equation form and the vertex form.
Mr parabola is very cruel now days. They now expect you to learn the basic form of,
TYPE 1: NORMAL CONCAVE UP PARABOLA.
Again we got (h, k) as our vertex.
But we got some new visitors! Mr Focal length, Mr Directrix. Better not confuse you, it's called the focal length and the directrix.
The focal length is
I won't introduced the latus rectum just yet.
Now the only way we can comprehend this is to practice.
Example 1.
In the parabola
a. The vertex: Easy, this can be read off it's
b. The focus: This is also easy. Recall the form
Match everything up. We need to find
THAT'S OUR LENGTH, NOT OUR FOCUS POINT!
The focus if you looked at the picture, it's above the vertex. In this case, the focal length was 4 units. It is 4 units above the vertex. Draw the vertex of (2, -3)
We can see the focus is 4 units above it. Hence (2, 1) is the focus point.
c. The directrix was
So the directrix is below the vertex. It maintains 4 units below the vertex. Hence the directrix is (2, -7). However the directrix is an equation of the line.
So
TYPE 2: NORMAL CONCAVE DOWN PARABOLA.
It is in the form of,
Example 2.
In the parabola
a. The vertex: Read off, (-4, -3).
b. The focus:
So the focal is,
Now,
Our vertex (-4, -3). So, 4 below (Since focus is inside parabola and it is concave down.) is the focus.
Our focus is (-4, -7).
c. The directrix: 4 places above your parabola. It's the line
TYPE 3: SIDEWAYS PARABOLA SMILING TO THE RIGHT.
It is in the form of,
Let's see an example.
Example 3.
Can you imagine me smiling to the right of the page? Oh wait. I don't smile. Anyway this parabola is sideways to the right.
If the parabola has an equation of
a. Vertex: Read off again! This time be careful. It's
b. Focus:
The focus is
So if we grab our vertex again
It's
We get that the focus is
c. Directrix: The directrix is outside the parabola. The focal length is
TYPE 4: SIDEWAYS PARABOLA SMILING TO THE LEFT.
It is in the form of,
Example 4.
If the parabola has an equation of
a. Vertex: Read off again, be careful. It's
b. Focus: We can see that
So
Our vertex was
c. Directrix: Outside the heart of the parabola, so
Try these:
State the vertex, focus and directrix in these equations and draw the parabola out.
1.
2.
3.
4.
Enough rambling. Feel free to ask me any questions and I will see if I can help you with understanding the latus rectum.
EDITING: Sorry for being slow, watching Disney's Enchanted.
[Note: Someone should check my working. It's after 9 pm, the time Spiral makes the most mistakes.]
Last edited:
Bored_of_HSC
Active Member
- Joined
- Jul 9, 2011
- Messages
- 1,498
- Gender
- Female
- HSC
- 2012
THE LOCUS
Example 1.
The locus, no it is not an insect. Basically you are given some conditions. For example,
A pointis always 3 units from the y axis. Find the locus.
The locus is the path or equation a point can take that satisfies the condition set.
In this case, the answer isor
.
See how its perpendicular distance is always 3 units from theaxis as you move along that path?
So the locus is just an equation that satisfies a specific set of conditions/path.
Try these:
1. Find the locus of a point (x, y) that is always 6 units from the y axis.
2. Find the locus of a point (x, y) that is always 4 units from the x axis.
Example 2.
If we were given some harder questions such as,
Find the locus of a point that moves in a plane such that. If
and
.
Woah! What?
Let's us comprehend this "seemingly tricky" phrase. It's basically asking for the path which P can travel such that as it travels, the distance. Still remember the distance formula?
First of all we need to find the distance ofto
.
Use the formula,
Now, let's find the distanceto
.
We must now equate them. Since they are the same distance from.
[That's your locus.]
Spiral tip: Draw these equations all of your graph, including your locus! You will see what is happening.
Try these:
Find the locus of a point P(x, y) in a plane such that PA = PB:
1. If A = (-2, 3), B = (4, 5)
2. If A = (1, 7), B = (4, -2)
3.
EDITING
I'm dedicating my 50th post to this guy, so i can finally rep him for helping peeps out.THE ANATOMY OF A PARABOLA
http://upload.wikimedia.org/wikipedia/commons/6/66/Parts_of_a_Parabola.JPG
Now. During Year 10 Mathematics when you are a baby your teacher told you there were three parts to a parabola right? The x intercept(s), the y intercept, the vertex and that was it. Now in Year 11 we can extend the definition of the parabola, we give it three more main parts, the focus, the directrix and the latus rectum.
Now you are use to the parabola as a smiley face and a sad face. We can extend the shape of the parabola into two more shapes, the sideways parabola. Kind of like a normal parabola but rotated to the left or right.
Okay back to business!
Your parabola equation can be written in two forms, the general equation form and the vertex form.
[Where
]
[Where
is our vertex and
]
Mr parabola is very cruel now days. They now expect you to learn the basic form of,
EDITING: Sorry for being slow, watching Disney's Enchanted.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Thank you human. My head spins around and around. I need to snack on some humans.I'm dedicating my 50th post to this guy, so i can finally rep him for helping peeps out.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Oh no! Did you mean the locus in the path of a parabola not the geometry of a parabola? Silly Spiral.
tambam
Member
- Joined
- Dec 31, 2010
- Messages
- 507
- Gender
- Female
- HSC
- 2011
You should just sign up for this online tutoring site, sponsored by maccas so its free.
http://www.mathsonline.com.au/
It's pretty good, covers all topics in depth.
And the guy has a really soothing voice and often tells you you're excellent, so its morale boosting too (Y)
http://www.mathsonline.com.au/
It's pretty good, covers all topics in depth.
And the guy has a really soothing voice and often tells you you're excellent, so its morale boosting too (Y)
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Almost all videos end with "excellent, good luck with your questions". By the way, your rabbit is delicious.You should just sign up for this online tutoring site, sponsored by maccas so its free.
http://www.mathsonline.com.au/
It's pretty good, covers all topics in depth.
And the guy has a really soothing voice and often tells you you're excellent, so its morale boosting too (Y)
I have tutoring already. Isn't one enough?You should just sign up for this online tutoring site, sponsored by maccas so its free.
http://www.mathsonline.com.au/
It's pretty good, covers all topics in depth.
And the guy has a really soothing voice and often tells you you're excellent, so its morale boosting too (Y)
juicystar07
Member
- Joined
- Feb 7, 2011
- Messages
- 203
- Gender
- Undisclosed
- HSC
- N/A
I swear @SpiralFlex, you are amazing. I can't wait until we see the ATAR scores, and we shall see your name next to the top mark, 99.95 
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
My name is sacred.I swear @SpiralFlex, you are amazing. I can't wait until we see the ATAR scores, and we shall see your name next to the top mark, 99.95
Uniqueness
Member
- Joined
- Feb 12, 2011
- Messages
- 352
- Gender
- Undisclosed
- HSC
- N/A
In example 3 type 3, since ^{2}= 2 \left ( x + \frac{5}{2} \right )) shouldn't the vertex be
shouldn't the vertex be ) ? Or did I do something wrong again?
? Or did I do something wrong again?
Hermes1
Banned
- Joined
- Oct 4, 2010
- Messages
- 1,282
- Gender
- Male
- HSC
- 2011
yeh ur right. spiral made a mistake. u can hardly blame him after all that working he had to do.In example 3 type 3, sinceshouldn't the vertex be
? Or did I do something wrong again?
tambam
Member
- Joined
- Dec 31, 2010
- Messages
- 507
- Gender
- Female
- HSC
- 2011
Haha, no its not actually tutoring, it just has videos/explanations for all the topics covered in all years of maths.I have tutoring already. Isn't one enough?
So it would be ideal in a situation like yours where you've missed a lesson on locus, you could just go watch the lesson & print out the summary on the website.
Then spiralflex would not have needed to type up that lengthy, albeit quite excellent, explanation.
& thank you, my bunny is awesome
juicystar07
Member
- Joined
- Feb 7, 2011
- Messages
- 203
- Gender
- Undisclosed
- HSC
- N/A
I bow down to you, SpiralFlex. Give me your wisdom! HAHAHAHAMy name is sacred.
