-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Complex Numbers (1 Viewer)
- Thread starter goobi
- Start date
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Good. Note: You must say equating real and imaginary coefficients otherwise you will not get the mark.x^2 - 2ixy + y^2 = 2i
x^2 + y^2 - i(2xy) = 2i
Equating to real and imaginary
x^2 + y^2 = 0
2xy = 2
Solve =)
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Also it's,
 for equating the imaginary part.
for equating the imaginary part.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Also it'sAhh yes my bad.
goobi
Member
- Joined
- Oct 6, 2010
- Messages
- 196
- Gender
- Male
- HSC
- 2012
I actually did attempt to solve these simultaneous equations. However, I got 4 values of x which was weird...x^2 - 2ixy + y^2 = 2i
x^2 + y^2 - i(2xy) = 2i
Equating to real and imaginary
x^2 - y^2 = 0
-2xy = 2
Solve =)
Can you please help me solve them if you can?
Thank you (and also the robot) for the help btw!
jnney
lemon
- Joined
- Mar 3, 2011
- Messages
- 1,437
- Gender
- Female
- HSC
- 2012
yeah, you get (x^2-1) (x^2+1) = 0
but x^2 + 1 = 0 is not part of the solution for x because you are only finding REAL roots
therefore x = - and + 1
you then sub these values back into your original simultaneous equations (say, xy=-1) to find the values of y.
you get : (1, -1) and (-1, 1)
but x^2 + 1 = 0 is not part of the solution for x because you are only finding REAL roots
therefore x = - and + 1
you then sub these values back into your original simultaneous equations (say, xy=-1) to find the values of y.
you get : (1, -1) and (-1, 1)
Last edited:
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
If Goobi is confused,
^2=2i) Where
Where 


Equating real and imaginary coefficients,
 (1)
(1)
 (2)
(2)
From (2),

Into (1),


(x^2+1)=0)

Where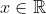

Where
Remember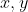 cannot take imaginary solutions because it belongs into the real set only!
cannot take imaginary solutions because it belongs into the real set only!
Equating real and imaginary coefficients,
From (2),
Into (1),
Where
Where
Remember
Last edited:
goobi
Member
- Joined
- Oct 6, 2010
- Messages
- 196
- Gender
- Male
- HSC
- 2012
yeah, you get (x^2-1) (x^2+1) = 0
but x^2 + 1 = 0 is not part of the solution for x because you are only finding REAL roots
therefore x = - and + 1
you then sub these values back into your original simultaneous equations (say, xy=-1) to find the values of y.
you get : (1, -1) and (-1, 1)
Ye i think you should get 2 values for x and 2 values for y.
Spi shall finish off the job, cos i might make a mistake again lols
Got it. Thanks!If Goobi is confused,
Where
Equating real and imaginary coefficients,
(1)
(2)
From (2),
Into (1),
Where
Where
Remembercannot take imaginary solutions because it belongs into the real set!
jnney
lemon
- Joined
- Mar 3, 2011
- Messages
- 1,437
- Gender
- Female
- HSC
- 2012
we are no longer in year 11.... >______<Oh have year 11's started 4 unit already!?
crap one year has gone by pretty quickly.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Hence why I believe 2012 cohort is going to be the best yet. Keen students.Oh have year 11's started 4 unit already!?
crap one year has gone by pretty quickly.
Let me eat you now.Got it. Thanks!
goobi
Member
- Joined
- Oct 6, 2010
- Messages
- 196
- Gender
- Male
- HSC
- 2012
Before eating me, would you like to have some Dim Sims as your first course?Let me eat you now.
Last edited:
kayven
Member
- Joined
- Jul 8, 2011
- Messages
- 69
- Gender
- Undisclosed
- HSC
- 2012
Oh My Gosh man. You guys are so smart at Maths, im in year 11 as well and i just tried and self teach myself basics of Complex Number. :'( Completing against you guys in Extension 2 Maths gives me shiver.
:O
Also, how much hours do you guys study daily?
:O
Also, how much hours do you guys study daily?

