HSC 2012 MX2 Marathon (archive) (4 Viewers)

Trebla · Feb 24, 2012

Re: 2012 HSC MX2 Marathon

$$Show that\\\\\displaystyle\int_0^{\frac{\pi}{2}}\dfrac{1+\sin x}{\cos x}\,dx = 1 + \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} +.....$

IamBread · Feb 24, 2012

Re: 2012 HSC MX2 Marathon

Trebla said:
$$Show that\\\\\displaystyle\int_0^{\frac{\pi}{2}}\dfrac{1+\sin x}{\cos x}\,dx = 1 + \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4}.....$

You changed the question?

IamBread · Feb 24, 2012

Re: 2012 HSC MX2 Marathon

IamBread said:
You changed the question?

Oh wait nevermind, just rewrote it

largarithmic · Feb 24, 2012

Re: 2012 HSC MX2 Marathon

Trebla said:
$$Show that\\\\\displaystyle\int_0^{\frac{\pi}{2}}\dfrac{1+\sin x}{\cos x}\,dx = 1 + \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4}.....$

uhhhhh... how can this be true? the right hand series (the harmonic series) diverges

IamBread · Feb 24, 2012

Re: 2012 HSC MX2 Marathon

Nevermind

Trebla · Feb 24, 2012

Re: 2012 HSC MX2 Marathon

largarithmic said:
uhhhhh... how can this be true? the right hand series (the harmonic series) diverges

Woops, almost thought I stumbled on something neat there which was why it was modified in the first place. Ah wells, I'll stick to the original question

$$Show that for $0 < x < \frac{\pi}{2}\\\\\displaystyle\int \dfrac{1+\sin x}{\cos x}\,dx = \displaystyle\sum_{n=1}^{\infty}\dfrac{\sin^nx}{n}+c$

3000th post!

cutemouse · Feb 25, 2012

Re: 2012 HSC MX2 Marathon

largarithmic said:
uhhhhh... how can this be true? the right hand series (the harmonic series) diverges

Hahahahah novice error by Trebla!

Trebla · Feb 25, 2012

Re: 2012 HSC MX2 Marathon

cutemouse said:
Hahahahah novice error by Trebla!

lol, I'm getting old...

someth1ng · Feb 25, 2012

Re: 2012 HSC MX2 Marathon

SpiralFlex said:
Ewwww

$\int -\frac{-2x}{2\sqrt{1-x^2}} \; dx$

$-\sqrt{1-x^2}+C$

I'm lost. I know that it works but how did you do it like that?

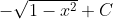
Carrotsticks · Feb 25, 2012

Re: 2012 HSC MX2 Marathon

someth1ng said:
I'm lost. I know that it works but how did you do it like that?

Substitution method u = 1-x^2.

After skipping a few steps too. Once you've done a fair few substitution method questions, you can jump from the question directly to the answer.

someth1ng · Feb 25, 2012

Re: 2012 HSC MX2 Marathon

Carrotsticks said:
Substitution method u = 1-x^2.

I see, how do you know which substitution to use? I probably don't have a chance at it since my school is doing some harder 3U topic first before integration.

Carrotsticks · Feb 25, 2012

Re: 2012 HSC MX2 Marathon

Usually, it is let u = *inside of the square root* for the basic questions.

Alternatively, you could let u^2 = inside of square root.

However you cannot blindly do this. You have to see that it can lead to the correct answer, and this can only be done by carefully observing the integral and doing lots of questions to familiarise yourself with such questions.

IamBread · Feb 25, 2012

Re: 2012 HSC MX2 Marathon

You should recognise it's almost f'(x)/sqrt[f(x)], and with a little manipulation you can get it there, once it's like that you can just quickly integrate. But as Carrotsticks said, you need to do a lot of questions to get yourself familiar to this.

Carrotsticks · Feb 25, 2012

Re: 2012 HSC MX2 Marathon

largarithmic said:
uhhhhh... how can this be true? the right hand series (the harmonic series) diverges

Some definite integrals can be divergent, one of the most trivial cases being:

$\int_{0}^{1}\frac{1}{x^{p}}, \qquad p \geq 1$

It just so happens that the one Trebla provided was convergent that it was not true.

Trebla, your question looks very interesting. Will try.

IamBread · Feb 25, 2012

Re: 2012 HSC MX2 Marathon

Trebla's question didn't work as at pi/2 it is undefined.

Carrotsticks · Feb 25, 2012

Re: 2012 HSC MX2 Marathon

IamBread said:
Trebla's question didn't work as at pi/2 it is undefined.

Trebla's original question with limits 0 --> pi/2 was actually convergent. Just because a point is undefined, does not necessarily mean that the area is automatically infinite.

For example, consider this integral:

$\int_{0}^{1} x^{p} dx \qquad 0 < p < 1$

The above integral in fact converges for all p E (0,1)

These integrals (sometimes called the p-integrals) are perfect examples of this.

Even though the function may not be defined, the area may well be.

An interesting figure sorta related to this is Gabriel's Horn: http://en.wikipedia.org/wiki/Gabriel's_Horn

Oh and I forgot to put the dx in the first p integral I provided.

IamBread · Feb 25, 2012

Re: 2012 HSC MX2 Marathon

That does make sense, though you wouldn't be able to figure it out using conventional methods, (as in you can't just sub the number in), which what I was trying to point out lol.

SpiralFlex · Feb 25, 2012

Re: 2012 HSC MX2 Marathon

IamBread said:
You should recognise it's almost f'(x)/sqrt[f(x)], and with a little manipulation you can get it there, once it's like that you can just quickly integrate. But as Carrotsticks said, you need to do a lot of questions to get yourself familiar to this.

This is the way.

math man · Feb 25, 2012

Re: 2012 HSC MX2 Marathon

someth1ng said:
I see, how do you know which substitution to use? I probably don't have a chance at it since my school is doing some harder 3U topic first before integration.

It was done using the reverse power
Rule, the best tool in 4u integration,
Substitution is hardly ever needed with
It

math man · Feb 25, 2012

Re: 2012 HSC MX2 Marathon

The reverse power rule is:
$\int f'(x)[f(x)]^{n} dx = \frac{f(x)^{n+1}}{n+1} + C$

HSC 2012 MX2 Marathon (archive) (4 Viewers)

Administrator

Member

Member

Member

Member

Administrator

Account Closed

Administrator

Retired Nov '14

Retired

Retired Nov '14

Retired

Member

Retired

Member

Retired

Member

Well-Known Member

Member

Member

Users Who Are Viewing This Thread (Users: 0, Guests: 4)