-
Looking for HSC notes and resources? Check out our Notes & Resources page
HSC 2012 MX2 Marathon (archive) (1 Viewer)
- Thread starter nightweaver066
- Start date
Nooblet94
Premium Member
- Joined
- Feb 5, 2011
- Messages
- 1,041
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
I occasionally do this just for fun, but obviously it's impossible cover everything that might come up. Is there anything specific you'd recommend having a look at?Furthermore, it doesn't hurt to look up a few out-of-syllabus things, as they often appear in the HSC.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: 2012 HSC MX2 Marathon
A simpler solution to the integration question:
https://docs.google.com/open?id=0B5x34d2OjtrQWlgwblItMGFUc0MzYUw3eG4zLWNodw
A simpler solution to the integration question:
https://docs.google.com/open?id=0B5x34d2OjtrQWlgwblItMGFUc0MzYUw3eG4zLWNodw
someth1ng
Retired Nov '14
Re: 2012 HSC MX2 Marathon
All of you guys are so..."keen"! I can't do any of these marathon questions...
All of you guys are so..."keen"! I can't do any of these marathon questions...
Re: 2012 HSC MX2 Marathon
None of those integration questions I put up? D:All of you guys are so..."keen"! I can't do any of these marathon questions...
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
Remember Spiral's three levels? Easy, Medium, Hard, Elite. That's 4...
Remember Spiral's three levels? Easy, Medium, Hard, Elite. That's 4...
Re: 2012 HSC MX2 Marathon
Are you saying they were elite?Remember Spiral's three levels? Easy, Medium, Hard, Elite. That's 4...
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
Lolcopters. No. I suggested to make 4 levels.Are you saying they were elite?
Re: 2012 HSC MX2 Marathon

Ok lol. You had me confused there.Lolcopters. No. I suggested to make 4 levels.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
^This is to make other students welcomed.
^This is to make other students welcomed.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
Ewwww
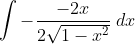
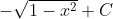
Ewwww
Re: 2012 HSC MX2 Marathon
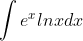
Haha I didn't think about doing it that way, turns out was easier then I expected. Here's one that I can't do, let's see if one of you can figure it out.Ewwww
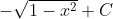
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
Use da powerfwul serreees
Use da powerfwul serreees
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
Some Conics...
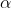\; $Let$\; a\;$ and $\;b \;$ be positive constants.$)

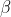\; $Consider the curve$ \; E_{1}: y=\sqrt{27-3x^2}, \; $where$ \; 0<x<3,\; $and the curve$\; E_{2}:y=\sqrt{9-\frac{x^2}{3}}\; $where$ \;0<x<3\sqrt{3})
 Find the point of intersection of \; $ \;E_{1} \; $and$ \; E_{2}\; \; \; \fbox{2})
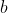 Let$ \; L\; $be the common tangent to $ \;E_{1} \; $and$ \; E_{2}\; \; \; ) .
.
 Find the equation of$\; L.\; \; \;\fbox{2})
 Find the area of the region bounded by $\;E_{1} \;, \; E_{2} \; $and$ \; L.\; \; \; \fbox{2})
Some Conics...
Nooblet94
Premium Member
- Joined
- Feb 5, 2011
- Messages
- 1,041
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
For part alpha I can't work out why m<0. I can see it must be the case for the rest of the question because of the domain.Some Conics...
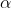\; $Let$\; a\;$ and $\;b \;$ be positive constants.$)
.
 Find the area of the region bounded by $\;E_{1} \;, \; E_{2} \; $and$ \; L.\; \; \; \fbox{2})
Re: 2012 HSC MX2 Marathon

Hmm I don't think I know enough on power series to get itUse da powerfwul serreees
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,473
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
Using Integration by Parts, we will acquire a very interesting integral:
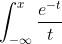
The power series expansion for this is fascinating, as it involves the Euler-Mascheroni Constant (denoted by a Gamma).
This series can be found by acquiring the Taylor series for the function:
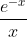
Then integrating the series term-by-term. iirc there is justification required for the convergence of the power series to the integral itself, but nothing too profound.
tl;dr can't do the question using HSC methods.
The integral of this cannot be done via elementary methods. I was actually playing around with this very same integral when I was doing MATH1903. One night I was thinking "What will happen if I combine the mutually inverse functions e^x and ln(x) ? Will my math book explode?", so I started working on it.Haha I didn't think about doing it that way, turns out was easier then I expected. Here's one that I can't do, let's see if one of you can figure it out.

Using Integration by Parts, we will acquire a very interesting integral:
The power series expansion for this is fascinating, as it involves the Euler-Mascheroni Constant (denoted by a Gamma).
This series can be found by acquiring the Taylor series for the function:
Then integrating the series term-by-term. iirc there is justification required for the convergence of the power series to the integral itself, but nothing too profound.
tl;dr can't do the question using HSC methods.
