SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
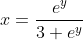
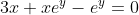
=-3x)
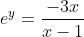
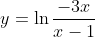
You do polynomial division.how would i find the inverse of y = e^x/(3 + e^x)
i get stuck on x(3+e^y) = e^y
I do not understand why you would need to find the inverse of the function.how would i find the inverse of y = e^x/(3 + e^x)
i get stuck on x(3+e^y) = e^y
dont know just trying to do what this sheet is askingI do not understand why you would need to find the inverse of the function.
EDIT: Oh it is unrelated to the differentiation question haha.
Umm, I don't think the average MX1 student will be able to *rigorously* prove the divergence of the Harmonic Series.<a href="http://www.codecogs.com/eqnedit.php?latex=\textsl{Prove that the series } 1@plus;\frac{1}{2}@plus;\frac{1}{3}@plus;\frac{1}{4}@plus;... \textsl{ diverges}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\textsl{Prove that the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+... \textsl{ diverges}" title="\textsl{Prove that the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+... \textsl{ diverges}" /></a>
This question is best suited to harder 3u, which is apart of the 4u course, not 3u, and yes as carrot said<a href="http://www.codecogs.com/eqnedit.php?latex=\textsl{Prove that the series } 1@plus;\frac{1}{2}@plus;\frac{1}{3}@plus;\frac{1}{4}@plus;... \textsl{ diverges}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\textsl{Prove that the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+... \textsl{ diverges}" title="\textsl{Prove that the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+... \textsl{ diverges}" /></a>
What about now:This question is best suited to harder 3u, which is apart of the 4u course, not 3u, and yes as carrot said
The proof is valid.What about now:
<a href="http://www.codecogs.com/eqnedit.php?latex=\textup{It is known that the series }1@plus;\frac{1}{2}@plus;\frac{1}{4}@plus;\frac{1}{8}... \textup{ converges to 2}. \\ \textup{By comparing the series } 1@plus;\frac{1}{2}@plus;\frac{1}{3}@plus;\frac{1}{4}... \textup{ to a geometric sequence where the ratio is not less than one, prove} \\\textup{that }1@plus;\frac{1}{2}@plus;\frac{1}{3}@plus;\frac{1}{4}... \textup{diverges}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\textup{It is known that the series }1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}... \textup{ converges to 2}. \\ \textup{By comparing the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}... \textup{ to a geometric sequence where the ratio is not less than one, prove} \\\textup{that }1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}... \textup{diverges}" title="\textup{It is known that the series }1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}... \textup{ converges to 2}. \\ \textup{By comparing the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}... \textup{ to a geometric sequence where the ratio is not less than one, prove} \\\textup{that }1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}... \textup{diverges}" /></a>
With a bit of thinking, a good 3U student (I think) should be able to get it but this proof might not be fully rigourous...
Is that sorta stuff like, allowed/used in 3u, when people dont really even know what converges/diverges mean?The proof is valid.
If there is some series A_n that diverges and there exists another series B_n such that B_n > A_n, then B_n also diverges.
Haha nws =)Is that sorta stuff like, allowed/used in 3u, when people dont really even know what converges/diverges mean?
Also, sorry man for not talking to you today outside the timetabling unit
<a href="http://www.codecogs.com/eqnedit.php?latex=y=x^n@plus;nx@plus;1\\ y'=nx^{n-1}@plus;n=n(x^{n-1}@plus;1)\\ $Stationary points occur when $y'=0\\ n(x^{n-1}@plus;1)=0\\ \therefore x^{n-1}=-1\\ $Hence, for there to be a stationary point with integer coordinates $n$ must be even since $n-1$ must be odd$\\ \therfore x=-1\\ y=(-1)^n@plus;n(-1)@plus;1\\ ~~~=1-n@plus;1$ (Since n is even)$\\ ~~~=2-n\\ \therefore $ the coordinates of the stationary point are $(-1,2-n)" target="_blank"><img src="http://latex.codecogs.com/gif.latex?y=x^n+nx+1\\ y'=nx^{n-1}+n=n(x^{n-1}+1)\\ $Stationary points occur when $y'=0\\ n(x^{n-1}+1)=0\\ \therefore x^{n-1}=-1\\ $Hence, for there to be a stationary point with integer coordinates $n$ must be even since $n-1$ must be odd$\\ \therfore x=-1\\ y=(-1)^n+n(-1)+1\\ ~~~=1-n+1$ (Since n is even)$\\ ~~~=2-n\\ \therefore $ the coordinates of the stationary point are $(-1,2-n)" title="y=x^n+nx+1\\ y'=nx^{n-1}+n=n(x^{n-1}+1)\\ $Stationary points occur when $y'=0\\ n(x^{n-1}+1)=0\\ \therefore x^{n-1}=-1\\ $Hence, for there to be a stationary point with integer coordinates $n$ must be even since $n-1$ must be odd$\\ \therfore x=-1\\ y=(-1)^n+n(-1)+1\\ ~~~=1-n+1$ (Since n is even)$\\ ~~~=2-n\\ \therefore $ the coordinates of the stationary point are $(-1,2-n)" /></a>Consider the equation y=x^n + nx + 1.
Find the condition such that the curve has a stationary point with integer co-ordinates.
Find the co-ordinates of the stationary point in terms of n.

Adding to that, show that the percentage error --> 0 as n approaches infinity.
Also adding on to part iii), find the percentage error of the approximate and actual area.
coulda done it for my test coming up next week if it wasnt cos inverse
Also adding on to part iii), find the percentage error of the approximate and actual area.
