nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
Last edited:
Ewww maffs.
LOL this came in our maths exam today, except it was show sin5pi/12:LLooks like we need more questions!
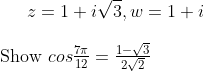
rolpsy's questionYou sure that question's right?
Uh thats not the riemann hypothesis...is the riemann hypothesis thing actually syllabus?
Very funny haha.Since we are on important mathematical problems, prove P is not NP.
