Esay Complex Number Question (2 Viewers)
- Thread starter CLD
- Start date
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
When in doubt, let z = x + iy
Let z = x + iy
 = |x + iy|)
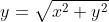

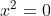
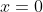
However |x^2 + y^2|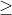 0, so the solution is the positive imaginary axis, i.e.
0, so the solution is the positive imaginary axis, i.e. 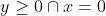
Let z = x + iy
However |x^2 + y^2|
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,662
- Gender
- Male
- HSC
- 2007
You are adding false solutions when you square both sides, the answer is just the non-negative half of the imaginary axis.When in doubt, let z = x + iy
Let z = x + iy
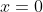
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
<3damn you nightweaver.
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
Ahh yeah that makes sense. Should be more careful..You are adding false solutions when you square both sides, the answer is just the non-negative half of the imaginary axis.
jnney
lemon
- Joined
- Mar 3, 2011
- Messages
- 1,437
- Gender
- Female
- HSC
- 2012
the top half of the y-axis.So, wait, what is the answer then?
So x=0??? but seaning said it is wrong?the top half of the y-axis.
jnney
lemon
- Joined
- Mar 3, 2011
- Messages
- 1,437
- Gender
- Female
- HSC
- 2012
sean is right. the x=0 IS the y=axis.So x=0??? but seaning said it is wrong?
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
the top half of the y-axis.
So x=0??? but seaning said it is wrong?
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
"Beware the twraps of modulus" quoted from my side-kick.
Okay but how can you sketch x=0 and y>(equal to)0 on one graph paper?
jnney
lemon
- Joined
- Mar 3, 2011
- Messages
- 1,437
- Gender
- Female
- HSC
- 2012
it's just a single line on the y=axis. Except:Okay but how can you sketch x=0 and y>(equal to)0 on one graph paper?
y>=0 is a condition which the graph x=0 must satisfy. it means that this particular graph does not extend below the origin.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
x=0 implies the entire Y axis.Okay but how can you sketch x=0 and y>(equal to)0 on one graph paper?
y greater than or equal to zero implies the top half of the xy plane (ie: Quadrants 1 and 2).
The only region satisfying both these conditions is the top half of the Y axis (including the origin).
umm what
Banned
umm what
Banned
http://community.boredofstudies.org/showthread.php?t=280133 can u do this plzzz 
x=0 implies the entire Y axis.
y greater than or equal to zero implies the top half of the xy plane (ie: Quadrants 1 and 2).
The only region satisfying both these conditions is the top half of the Y axis (including the origin).
school4nerds
Member
- Joined
- Oct 13, 2011
- Messages
- 131
- Gender
- Female
- HSC
- 2012
let z= x+iy,
Im(z)= y
|z|= (sqrt)(x^2 + y^2)
y^2= x^2+y^2
x^2=0
x=0
why is this wrong? i thought you could square both sides? :\
Im(z)= y
|z|= (sqrt)(x^2 + y^2)
y^2= x^2+y^2
x^2=0
x=0
why is this wrong? i thought you could square both sides? :\
