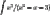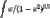Saturn WY15
Member
- Joined
- May 21, 2010
- Messages
- 129
- Gender
- Male
- HSC
- 2012
How do you do this question \int x^3/(x^2-x-3) ? Thanks, a better picture of the question is in the attachment
Attachments
-
741 bytes Views: 97