asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,225
- Gender
- Undisclosed
- HSC
- 2012
Either my setup is completely wrong or I'm way too tired. The area from x=0 to x=2 between the curve 4y=x^2 and its directrix is rotated about its directrix. Using shells, show the volume of the solid generated is  .
.
^2-(1+y)^2)x \\ = \pi((1+y)^2+2(1+y)\delta y + (\delta y)^2 -(1+y)^2)x \\ = 2\pi (1+y)\delta y x \\ = 4\pi(1+y)\delta y \sqrt{y} \\ = 4\pi(\sqrt{y}+y\sqrt{y}) \delta y)
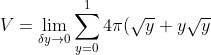\delta y\\ =4\pi \int_0^1 y^{\frac{1}{2}}+y^{\frac{3}{2}} dy \\ = 4 \pi (\frac{2y^{\frac{3}{2}}}{3}+\frac{2y^{\frac{5}{2}}}{5}) \right]_{0}^{1} \\ = 4\pi(\frac{2}{3}+\frac{2}{5} \\ = \frac{64\pi}{15})
\\ = 4\pi \left \frac{2y^{\frac{3}{2}}{3}+\frac{2y^{\frac{5}{2}}{5} \right]_{0}^{1} \\ = 4\pi(\frac{2}{3}+\frac{2}{5}) \\ = \frac{64\pi}{15}
\\ = 4\pi \left \frac{2y^{\frac{3}{2}}{3}+\frac{2y^{\frac{5}{2}}{5} \right]_{0}^{1} \\ = 4\pi(\frac{2}{3}+\frac{2}{5}) \\ = \frac{64\pi}{15}
Last edited:


