Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
So I had formed a hypothesis that:
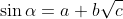
Where alpha is any integer degree.
Could I write the sine of that angle, be it any angle, in exact form
And a, b and c are all integers.
Now the above RHS is probably wrong (maybe not)
But Im just wondering if it could be done, if so is it possible to prove it? If it is wrong, can someone make an expression similar to what I have done that fits all criteria for any angle alpha, be it an integer.
And also is it possible to do this for any rational number?
Is it possible to do this even with an irrational alpha?
Ive just been wondering, and I know the maths part of BoS are really smart, so Im expecting a great solution to this
Thanks
Where alpha is any integer degree.
Could I write the sine of that angle, be it any angle, in exact form
And a, b and c are all integers.
Now the above RHS is probably wrong (maybe not)
But Im just wondering if it could be done, if so is it possible to prove it? If it is wrong, can someone make an expression similar to what I have done that fits all criteria for any angle alpha, be it an integer.
And also is it possible to do this for any rational number?
Is it possible to do this even with an irrational alpha?
Ive just been wondering, and I know the maths part of BoS are really smart, so Im expecting a great solution to this
Thanks
