Ok, in reality what we do is we test both negative
and positive large values, the thing is, for certain functions it is redundant to test negative large values because we know they dont work.
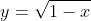
We know that any large positive value wont work, we test a large negative value and we get a large positive y value. So for example
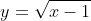
, any value of x less than 1 will not work (so any large negative wont work) we dont test this because we dont need to, because we know we will get math error if we put it in the calculator.
Negative large values (as they approach to neg infinity), are part of the x values of the graph itself.
Now this is important, if we look at the domain x>1, this means that x
can be any value BUT it must be greater than 1, is 0 part of this domain? No
Is -1 part of this domain? No, is negative infinity part of this domain? no, BUT positive infinity is, you can think of it like this: the domain for x>1 is from 1 to positive infinity, so pos infinity is counted.
Testing pos/neg infinity is testing very large values on your calculator, they arent really that random, but rather they are there so we can get an idea of how the curve looks like.
For the curve
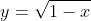
, you are right with the logic of the domain. Now for the range, it is always greater than or equal to 0. This is because, the
result of a square root is always positive, so no matter how big our x goes (or how small within its domain), our y will always be greater than or equal to zero, hence our range is as such.
To test large negative values, take x=-100, we get
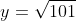
. They will never ask you to plot this, nor do you need to, what this shows us is that when you get a very large negative value of x, we get a large (but a much smaller) value for y which is positive. This concept is best shown graphically.
So we find intercepts, starting point of square root function and the domain and range, we test a large positive or negative value. From this information, start to sketch from the starting point, through our intercepts. Now looking at the points we tested sqrt(101)=10.something. So although we have an incredibly big x value we only get a 'little' big y value, so our curve will look like such.
hence our curve goes through the 2nd quadrant (the section of positive y negative x), but its closer to the x axis than the y.

