michaeljennings
Active Member
Hey guys how would you prove the following..
SQRT(n) +1/SQRT(n+1) > SQRT(n+1)
cheers =)
SQRT(n) +1/SQRT(n+1) > SQRT(n+1)
cheers =)
hah i was just about to delete this because i figured out the answer, thanks for the assistance though =)So assuming there's no tricks, like n can be a negative number or we allow complex values...
And:
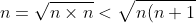})
well actually n wasnt allowed to be negative its for n>1 (should have stated that originally)How'd you do it?
From where did your first expressionwell actually n wasnt allowed to be negative its for n>1 (should have stated that originally)
what i did was change the LHS to [SQRT(n^2+n) + 1/SQRT(n+1)] which happens to be greater than (n+1)/SQRT(n+1) since SQRT(n^2+n) > n
therefore [SQRT(n^2+n) + 1/SQRT(n+1)] > SQRT(n+1) using (n+1)/SQRT(n+1) = SQRT(n+1)
as you can see i dont know how to use latex hah
You are a second/third year university student, who prides himself on his 'mathematical abilities', yet you take the poor-man's way out to doing this question, by starting with the given identity then using 'iff' steps. Although it technically is correct, surely somebody of your 'calibre' could muster up a better proof.So assuming there's no tricks, like n can be a negative number or we allow complex values... the gist of it (to me) is:
And:
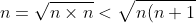})
The sqrt(n^2+n) + 1 is all on top of the denominator.From where did your first expressioncome? The term was originally \sqrt{n}, which is not the same as \sqrt{n^2+n}.
You are a second/third year university student, who prides himself on his 'mathematical abilities', yet you take the poor-man's way out to doing this question, by starting with the given identity then using 'iff' steps. Although it technically is correct, surely somebody of your 'calibre' could muster up a better proof.
The terms were not bracketed, and I mis-interpreted his intended expression.The sqrt(n^2+n) + 1 is all on top of the denominator.
No need to flame. You could have said, "Alternatively here is a better method to approach the proof" which would be more helpful to Shadowdude.
That doesn't mean you should attack him everytime he makes a post on this forum. Unlike the non-school forums, I expect discussion in the school forums to be more civilised. As long as the post is appropriate, there is no need to flame regardless of who the user is. I don't mind/care if you dislike Shadowdude, but there is no need to vent your dislike of him at every unprovoked opportunity (especially on the school forums). I appreciate constructive criticism on these forums, but this is not what you offered.The terms were not bracketed, and I mis-interpreted his intended expression.
Take a look at Shadowdude's posting history on anything Mathematics related, and you will understand the 'need to flame'. People who brag about their abilities, even though they may possess great abilities, are already disliked. People who brag about their great abilities, when they in fact have no abilities, are even more disliked. Unfortunately, Shadowdude is infamous for the latter and you will see this within a few weeks of regular posting here.
