SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Re: HSC 2013 4U Marathon
Nice question Sy.
Nice question Sy.
Very good, a different approach to what I had in mind for the second one however. The third one is straightforward when b=3a then there is a horizontal point of inflection at x=1.still editing
Edit: sorry, got to study for English now, someone feel free to take over lol.
Well the really hard ones should probably not be. For example my triangular numbers question should be in this thread imo (or 3U one)2U questions should be placed in the 2U thread. I'll post a question in a few minutes.
Err yeah sure I guess, it isnt my strength but practise makes perfect.Would you like circle geometry problems?
4U circle isn't any real extra theorems, it's just harder problems to 3U.
urgh so tired of belongingVery good, a different approach to what I had in mind for the second one however. The third one is straightforward when b=3a then there is a horizontal point of inflection at x=1.
Can someone else post a question now? (preferably Complex and Polynomials, (or also anything that can be done with 2U))
M8 this question cost you a generation of babies + you know.Actually I just remembered an awesome question (aye aye spiral)
Ifare all distinct positive integers, find what they are so that:
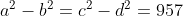
No, YOU cost me.M8 this question cost you a generation of babies + you know.
I just found a mistake in my question, when I did it I divided the an inequality by b, which is not allowed since that is assuming b>0 there is indeed two domains for b such that there are 3 real roots.urgh so tired of belongingHow come
though?
Anyway here's a difficult complex/circle geo question that keeps propping up everywhere lol

But! The mistake was critical if I had gotten is right you wouldn't be how you say "IN" at the moment.No, YOU cost me.
You were the one who got it wrong.
wait wat.But! The mistake was critical if I had gotten is right you wouldn't be how you say "IN" at the moment.
Assuming a, and b real:i) Show that
ii) Consider the quadraticwhere the co-efficients are all positive.
If the roots are both complex, show that
iii) If one of the roots is, deduce that:
^2 + y^2 > 2)
There's another way to do this problem using mappings in complex analysis. It's WAY more elegant.
nice work! Another way is to use exterior angle of a cyclic quad or angles in the same segment to prove arg(1/z3-1/z1)=arg(1/z2-1/z1)
Woops, just realised in my working out I forgot a minus sign, which lead to my result.Are you sure the last result is correct?

