-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
HSC 2013 MX2 Marathon (archive) (4 Viewers)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,662
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
 .
.
Yes but the existence and uniqueness of a MINIMAL polynomial is not immediately clear and must be proven. And thanksNice work, it can also be done by considering the geometric series:
Substituting cis theta, equating real parts for a series in cosine. Then integrating with bounds alpha and pi yields the LHS and the RHS plus a limit to infinity of an integral which one must prove converges to zero.
Ah alright, is that not a definition of an algebraic number? To be a root of a rational polynomial?
Also your method is very clever.
Registered User
Member
- Joined
- May 4, 2013
- Messages
- 110
- Gender
- Male
- HSC
- N/A
Re: HSC 2013 4U Marathon
I found this question in a book called
 .
.
Nice work but I don't know how we can prove that the limit goes to 0. There is a more rigorous method to prove this, will post it sometime next week.Using the result from the previous question:
Integrating both sides from pi to 2, and using the double angle rule, the result from the Basel problem and so on, we arrive at:
Then noticing that
We can notice that the LHS of what I have right now, is the LHS of the question - 1 (since at k=0 the function approaches 1). This then cancels out the term on the RHS, therefore leaving it with:
I know that it should evaluate to zero, however the same problem from when I encountered trying the Basel problem comes up where I cannot justify interchanging the theta integral and the limit to infinity as the alpha integral converges to zero due to by parts. However I cannot justify putting it in there unfortunately :/
I found this question in a book called
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
~ln(Bx)~dx)
Registered User
Member
- Joined
- May 4, 2013
- Messages
- 110
- Gender
- Male
- HSC
- N/A
Re: HSC 2013 4U Marathon


Working on this.
Last edited:
Registered User
Member
- Joined
- May 4, 2013
- Messages
- 110
- Gender
- Male
- HSC
- N/A
Re: HSC 2013 4U Marathon

!}{n!(m-k)!} = \frac{n+1}{n-m+1})
Edit:
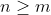
Edit:
Last edited:
Registered User
Member
- Joined
- May 4, 2013
- Messages
- 110
- Gender
- Male
- HSC
- N/A
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
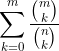
And I don't know how to do that :/
Telescoping, pairing, binomial theorem don't seem to work
Possibly a combinatoric proof?
I suck at those but yeah
EDIT:
Considering the cards of numbers 1, 2, 3, 4, ... , m, .... , n on the table.
We must pick k cards from the n on the table.
The probability that we pick these k cards from the first m is
 = \frac{\binom{m}{k}}{\binom{n}{k}} )
So summing these probabilities will give us the LHS.
Now is there a nice way of doing this probability a different way to yield the RHS?
It becomes:
And I don't know how to do that :/
Telescoping, pairing, binomial theorem don't seem to work
Possibly a combinatoric proof?
I suck at those but yeah
EDIT:
Considering the cards of numbers 1, 2, 3, 4, ... , m, .... , n on the table.
We must pick k cards from the n on the table.
The probability that we pick these k cards from the first m is
So summing these probabilities will give us the LHS.
Now is there a nice way of doing this probability a different way to yield the RHS?
Last edited:
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
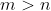
Although I think the question should state that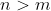 otherwise it won't work.
otherwise it won't work.
What ifIt becomes:
And I don't know how to do that :/
Telescoping, pairing, binomial theorem don't seem to work
Possibly a combinatoric proof?
I suck at those but yeah
EDIT:
Considering the cards of numbers 1, 2, 3, 4, ... , m, .... , n on the table.
We must pick k cards from the n on the table.
The probability that we pick these k cards from the first m is
So summing these probabilities will give us the LHS.
Now is there a nice way of doing this probability a different way to yield the RHS?
Although I think the question should state that
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Well yeah if m > n then we arrive at negative factorials so it should be discounted.What if
Although I think the question should state thatotherwise it won't work.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
maybe you can choose the cards in this way some how.
Which is equal to:
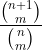
The RHS is equal to (n+1)P(m) / (n)P(m) (idk how to do permutations in latex)Well yeah if m > n then we arrive at negative factorials so it should be discounted.
maybe you can choose the cards in this way some how.
Which is equal to:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
So that can mean that when counting the probability the different all the cards needs to be on the table at once. And we need to find the probability of selecting the cards in that fashion among the m sets of (1,2,...,n) cards in one go (because there is only one fraction).
And for permutation, I guess you can do:
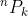
Nice observation.The RHS is equal to (n+1)P(m) / (n)P(m) (idk how to do permutations in latex)
maybe you can choose the cards in this way some how.
Which is equal to:
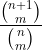
So that can mean that when counting the probability the different all the cards needs to be on the table at once. And we need to find the probability of selecting the cards in that fashion among the m sets of (1,2,...,n) cards in one go (because there is only one fraction).
And for permutation, I guess you can do:
Registered User
Member
- Joined
- May 4, 2013
- Messages
- 110
- Gender
- Male
- HSC
- N/A
Last edited:
Registered User
Member
- Joined
- May 4, 2013
- Messages
- 110
- Gender
- Male
- HSC
- N/A
Re: HSC 2013 4U Marathon

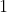 \frac{bc}{a}+\frac{ac}{b}+\frac{ab}{c}\geqslant (a+b+c))
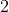 \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\geqslant \frac{1}{\sqrt{bc}}+\frac{1}{\sqrt{ca}})
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,509
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
2/a^2 + 2/b^2 + 2/c^2 -2[(1/ab)+(1/bc)+(1/ac)] >=0
=> (1/a)^2 + (1/b)^2 + (1/c)^2 >= 1/bc + 1/ac + 1/ab for all real a,b,c=/=0 (*)
Hence, bc/a + ac/b + ab/c = abc[(1/a^2)+(1/b^2) +(1/c^2)]>=abc[(1/ab)+(1/bc)+(1/ac)]=a+b+c as req.
2) Refer back to (*), replace a with sqrt(a), b with sqrt(b) and c with sqrt(c) and the second inequality immediately falls out for a,b,c>0
Sorry if it's hard to read, still haven't learnt latex.
1) [(1/a)-(1/b)]^2 + [(1/a)-(1/c)]^2 + [(1/b)-(1/c)]^2 >=0 (equality occurs iff a=b=c)
2/a^2 + 2/b^2 + 2/c^2 -2[(1/ab)+(1/bc)+(1/ac)] >=0
=> (1/a)^2 + (1/b)^2 + (1/c)^2 >= 1/bc + 1/ac + 1/ab for all real a,b,c=/=0 (*)
Hence, bc/a + ac/b + ab/c = abc[(1/a^2)+(1/b^2) +(1/c^2)]>=abc[(1/ab)+(1/bc)+(1/ac)]=a+b+c as req.
2) Refer back to (*), replace a with sqrt(a), b with sqrt(b) and c with sqrt(c) and the second inequality immediately falls out for a,b,c>0
Sorry if it's hard to read, still haven't learnt latex.
Last edited:
shongaponga
Member
- Joined
- Feb 15, 2012
- Messages
- 125
- Gender
- Male
- HSC
- 2012
Re: HSC 2013 4U Marathon
http://www.codecogs.com/latex/eqneditor.php Use this website, then simply copy and paste the code generated and wrap it around [ tex ] "CODE" [ / tex ] (without the spaces).1) [(1/a)-(1/b)]^2 + [(1/a)-(1/c)]^2 + [(1/b)-(1/c)]^2 >=0 (equality occurs iff a=b=c)
2/a^2 + 2/b^2 + 2/c^2 -2[(1/ab)+(1/bc)+(1/ac)] >=0
=> (1/a)^2 + (1/b)^2 + (1/c)^2 >= 1/bc + 1/ac + 1/ab for all real a,b,c=/=0 (*)
Hence, bc/a + ac/b + ab/c = abc[(1/a^2)+(1/b^2) +(1/c^2)]>=abc[(1/ab)+(1/bc)+(1/ac)]=a+b+c as req.
2) Refer back to (*), replace a with sqrt(a), b with sqrt(b) and c with sqrt(c) and the second inequality immediately falls out for a,b,c>0
Sorry if it's hard to read, still haven't learnt latex.
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,509
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
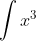
Last edited:
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,509
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Did it. ^ That happened.http://www.codecogs.com/latex/eqneditor.php Use this website, then simply copy and paste the code generated and wrap it around [ tex ] "CODE" [ / tex ] (without the spaces).
Makematics
Well-Known Member
Re: HSC 2013 4U Marathon
oooo i also wanna learn how to use LaTex
oooo i also wanna learn how to use LaTex
- Status
- Not open for further replies.

