asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,225
- Gender
- Undisclosed
- HSC
- 2012
There is some theory called the 'p integrals' and explains that that for p>1, the integral  The point is that the successive parts being added are getting smaller and smaller at a fast enough rate so that the total area is finite.
The point is that the successive parts being added are getting smaller and smaller at a fast enough rate so that the total area is finite.
The length of a curve) is given by
is given by 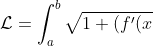)^2}\mathop{dx}.) Which is derived from pythagoras' theorem essentially. In terms of velocity/accel it doesn't have any significance.
Which is derived from pythagoras' theorem essentially. In terms of velocity/accel it doesn't have any significance.
If there constants were different the world would still function just in a different way. This is more of a philosophical question.
The length of a curve
If there constants were different the world would still function just in a different way. This is more of a philosophical question.
Last edited:
