juantheron
Active Member
- Joined
- Feb 9, 2012
- Messages
- 259
- Gender
- Male
- HSC
- N/A
Re: MX2 Integration Marathon
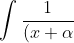^{1+\frac{1}{n}}\cdot (x+\beta)^{1-\frac{1}{n}}}dx = \int \frac{1}{\left(\frac{x+\alpha}{x+\beta}\right)^{1+\frac{1}{n}}}\cdot \frac{1}{(x+\beta)^2}dx)
 = t$\;,then \; $\displaystyle \frac{1}{(x+\beta)^2}dx = \frac{1}{(\beta-\alpha)}dt$)
}\int \frac{1}{t^{1+\frac{1}{n}}}dt = \frac{1}{(\beta-\alpha)}\int t^{-1-\frac{1}{n}}dt $)
}\cdot \frac{t^{-\frac{1}{n}}}{-\frac{1}{n}}+\mathbb{C} = \frac{1}{(\beta-\alpha)}\cdot -n \cdot \frac{1}{t^{\frac{1}{n}}}+\mathbb{C}$)
$)
-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
HSC 2012-14 MX2 Integration Marathon (archive) (6 Viewers)
- Thread starter bleakarcher
- Start date
- Status
juantheron
Active Member
- Joined
- Feb 9, 2012
- Messages
- 259
- Gender
- Male
- HSC
- N/A
Re: MX2 Integration Marathon
^{10}}dx$)
\sqrt{1+x^4}}dx$)
\sqrt{1+x^4}}dx$)
\cdot \tan^3 x}dx$)
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Last edited:
Re: MX2 Integration Marathon
^2 (x^2-1)}{(x^2+1)^2 \sqrt{x^4+x^2+1}} )
Dividing by
(Note this is assuming  )
 (1-\dfrac{1}{x^2})}{(x+\dfrac{1}{x})^2 \sqrt{x^2+1+\dfrac{1}{x^2}}} )
^2 (x^2-1)}{(x^2+1)^2 \sqrt{x^4+x^2+1}} dx )
 (1-\dfrac{1}{x^2})}{(x+\dfrac{1}{x})^2 \sqrt{x^2+1+\dfrac{1}{x^2}}} dx )
Use substitution=x+\dfrac{1}{x} )
 \tan(z) \cdot dz =(1-\dfrac{1}{x^2})\cdot dx )
+2) (\sec(z) \tan(z)) \cdot dz}{(\sec(z))^2 \sqrt{\sec^2 (z)-1}} )
+2}{\sec(z)} \cdot dz )
+c )
Where and substitute back into x...
Dividing by
Use substitution
Where
Last edited:
Re: MX2 Integration Marathon
}{x} )
yields the integral:
(Partial Fractions)
 )
^2+\frac{1}{2}}+\dfrac{1}{(u-\frac{1}{\sqrt{2}})^2+\frac{1}{2}} \cdot du )
+\tan^{-1}(u\sqrt{2}-1)]+c )
 )
)+c )
Where and substitute back in terms of x...
Using the substitutionView attachment 30314 Made this one up
Where
Last edited:
Re: MX2 Integration Marathon
Yeh sweetpretty much what i did
juantheron
Active Member
- Joined
- Feb 9, 2012
- Messages
- 259
- Gender
- Male
- HSC
- N/A
Re: MX2 Integration Marathon
^2}dx$)
^{17}\cdot (5x-3)dx$)
juantheron
Active Member
- Joined
- Feb 9, 2012
- Messages
- 259
- Gender
- Male
- HSC
- N/A
Re: MX2 Integration Marathon
 }{(1-t^2)\cdot (1+t^2)\cdot (1-3t^2)}dt$)
}{(1-u)\cdot(1+u)\cdot(1-3u)}du = \frac{1}{3}\int\frac{3u-u^2}{(u-1)\cdot (u+1)\cdot(u-\frac{1}{3})}du$)
Last edited:
Re: MX2 Integration Marathon
^2}dx )
Let
^2 (\dfrac{1}{\sqrt{1+t^2}})2 }{((\dfrac{2t}{\sqrt{1+t^2}})^3 +(\dfrac{1}{\sqrt{1+t^2}})^3 )^2}\cdot \dfrac{dt}{1+t^2} )
^2} \cdot dt )
} +c )
For 2nd question so far i can only think of expanding ahahaha, which isnt to long if we leave it in sigma notation
Nice question, works out very neatly
Let
For 2nd question so far i can only think of expanding ahahaha, which isnt to long if we leave it in sigma notation
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
- Status