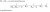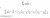-
Looking for HSC notes and resources? Check out our Notes & Resources page
HSC 2014 MX2 Marathon ADVANCED (archive) (4 Viewers)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
By the sine rule (this isn't always stated as part of the sine rule, but it is easy to prove with HSC circle geometry):
}=\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)}=2R.)
So, making the substitutions:,t=\sin(\beta),u=\cos(\alpha),v=\cos(\beta)) we get
we get
}}=R\cdot\frac{s^2+t^2}{\sqrt{s^2+t^2+2st\cos(\pi-(\alpha+\beta))}})
}}.)
So it is sufficient to show that the second factor in this last line is smaller that 1.
^2\geq 0)
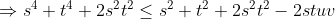
}}\leq 1.)
I solved it, but it's a pretty dirty solution lol. Anyway, better than nothing.Whoops, my first inequality is wrong. I still get the feeling that there is a short solution from that first expression though, I will try again after netball.
No, I wish!
By the sine rule (this isn't always stated as part of the sine rule, but it is easy to prove with HSC circle geometry):
So, making the substitutions:
So it is sufficient to show that the second factor in this last line is smaller that 1.
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
So solutions are either constant or of degree k.
For k=0 P=1 is trivially the only solution. For k=1, any constant is a solution. For k > 1, the only constant solutions are 0 and 1.
We can now assume k > 0 and just look for the non-constant solutions (which must be of degree k).
Write
=ax^k+Q(x))
with
<k .)
Putting this in the original equation we get
P(x)^k+Q(P(x))=0.)
By degree considerations, this forces a=1 (if the first term is nonzero, nothing in the second is of high enough degree to cancel it out) and then Q=0.
So the only such non-constant solution is=x^k.)
Comparing degrees we get deg(P)^2 = k*deg(P).Another one, I can post my solution to the last question if requested:
 \ $such that$ \\ P(P(x)) = (P(x))^k )
So solutions are either constant or of degree k.
For k=0 P=1 is trivially the only solution. For k=1, any constant is a solution. For k > 1, the only constant solutions are 0 and 1.
We can now assume k > 0 and just look for the non-constant solutions (which must be of degree k).
Write
with
Putting this in the original equation we get
By degree considerations, this forces a=1 (if the first term is nonzero, nothing in the second is of high enough degree to cancel it out) and then Q=0.
So the only such non-constant solution is
integral95
Well-Known Member
- Joined
- Dec 16, 2012
- Messages
- 779
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon - Advanced Level
Yeah lol so like no one seems to be responding to the integration marathon so i thought i might post it here.
^n dx = \frac{m!n!}{(m+n+1)!}\\ \\ Find \int \frac{x^2-1}{x^2+1}\frac{1}{\sqrt{1+x^4}} dx )
For the second integral there's a hint that the substitution would help, but you could use another method if you can come up with one
would help, but you could use another method if you can come up with one 
Yeah lol so like no one seems to be responding to the integration marathon so i thought i might post it here.
For the second integral there's a hint that the substitution
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon - Advanced Level
Don't reveal the substitution, that takes all the fun away :/Yeah lol so like no one seems to be responding to the integration marathon so i thought i might post it here.
For the second integral there's a hint that the substitutionwould help, but you could use another method if you can come up with one

Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon - Advanced Level
 \geq (a^2+b^2)^2 \\ \\ $By dividing the triangle into 3 by its circumcentre, and looking at the isocoles triangle with angle$ \ 2C \ $we get$ \ c = 2R \sin C \\ \\ $So$ \ 4R^2 = \frac{a^2+b^2 - 2ab\cos C}{1 - \cos^2 C} \\ \\ $So it is needed to prove$ \\ \\ (a^2+b^2 + 2ab\cos C)(a^2+b^2-2ab\cos C) \geq (a^2+b^2)^2 - \cos^2 C (a^2+b^2)^2 \\ \\ $Expanding out we get$ \\ \\ (a^2+b^2)^2 \geq 4a^2b^2 \Rightarrow \ (a^2-b^2)^2 \geq 0 \ \square )
Yep exactly my solution
Here was my solution:I solved it, but it's a pretty dirty solution lol. Anyway, better than nothing.
By the sine rule (this isn't always stated as part of the sine rule, but it is easy to prove with HSC circle geometry):
So, making the substitutions:we get
So it is sufficient to show that the second factor in this last line is smaller that 1.
}}\leq 1.)
Comparing degrees we get deg(P)^2 = k*deg(P).
So solutions are either constant or of degree k.
For k=0 P=1 is trivially the only solution. For k=1, any constant is a solution. For k > 1, the only constant solutions are 0 and 1.
We can now assume k > 0 and just look for the non-constant solutions (which must be of degree k).
Write
with
Putting this in the original equation we get
By degree considerations, this forces a=1 (if the first term is nonzero, nothing in the second is of high enough degree to cancel it out) and then Q=0.
So the only such non-constant solution is=x^k.)
Yep exactly my solution
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
What I can prove though, is that the only continuous solutions are constant.
Because if we let c:=f(0), then for x in (-1,1) we have
=f(x^{2^n}))
for any positive integer n. But for such x,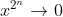 which means by continuity that the RHS tends to c. As the LHS is constant in n, we are forced to conclude that this constant is c.
which means by continuity that the RHS tends to c. As the LHS is constant in n, we are forced to conclude that this constant is c.
So we know that f(x)=c on the interval (-1,1). This also implies by continuity that f(1)=c.
We can do something similar with square roots to show that for x > 1, we have=f(x^{1/2^n})\rightarrow f(1)= c) , so f(x) = c for all x >1 (so we have now shown that f(x) = c at all positive reals).
, so f(x) = c for all x >1 (so we have now shown that f(x) = c at all positive reals).
Finally, for negative x, x^2 is positive. So f(x)=f(x^2)=c.

Isn't the function that is 1 at 0 and 0 elsewhere a non-constant solution?
What I can prove though, is that the only continuous solutions are constant.
Because if we let c:=f(0), then for x in (-1,1) we have
for any positive integer n. But for such x,
So we know that f(x)=c on the interval (-1,1). This also implies by continuity that f(1)=c.
We can do something similar with square roots to show that for x > 1, we have
Finally, for negative x, x^2 is positive. So f(x)=f(x^2)=c.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon - Advanced Level
And yes you got it (can you please post a problem)
Ah yes I meant continuousIsn't the function that is 1 at 0 and 0 elsewhere a non-constant solution?
What I can prove though, is that the only continuous solutions are constant.
Because if we let c:=f(0), then for x in (-1,1) we have
for any positive integer n. But for such x,which means by continuity that the RHS tends to c. As the LHS is constant in n, we are forced to conclude that this constant is c.
So we know that f(x)=c on the interval (-1,1). This also implies by continuity that f(1)=c.
We can do something similar with square roots to show that for x > 1, we have, so f(x) = c for all x >1 (so we have now shown that f(x) = c at all positive reals).
Finally, for negative x, x^2 is positive. So f(x)=f(x^2)=c.

And yes you got it (can you please post a problem)
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
.)
Sure. Show that:Ah yes I meant continuous
And yes you got it (can you please post a problem)
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon - Advanced Level
α+β+γ=180 -> cot(α+β)=-cot(γ)
[cot(α)cot(β)-1]/[cot(α)+cot(β)] = -cot(γ)
cot(γ)/[cot(α)+cot(β)] = cot^2(γ)/[cot(α)cot(β)-1] = [-sin(α)sin(β)cos^2(γ)]/[sin^2(γ)cos(α+β)] = [sin(α)sin(β)cos(γ)]/sin^2(γ)
But, cos(γ) = [a^2+b^2-c^2]/2ab = [c^2(k-1)]/2ab (Given a^2+b^2=kc^2)
∴ cot(γ)/[cot(α)+cot(β)] = [c^2(k-1)sin(α)sin(β)]/[2absin^2(γ)]
Since sin(α)/a = sin(β)/a = sin(γ)/c;
cot(γ)/[cot(α)+cot(β)] = [c^2(k-1)]/2 x sin(γ)/c x sin(γ)/c x 1/sin^2(γ) = (k-1)/2
α+β+γ=180 -> cot(α+β)=-cot(γ)
[cot(α)cot(β)-1]/[cot(α)+cot(β)] = -cot(γ)
cot(γ)/[cot(α)+cot(β)] = cot^2(γ)/[cot(α)cot(β)-1] = [-sin(α)sin(β)cos^2(γ)]/[sin^2(γ)cos(α+β)] = [sin(α)sin(β)cos(γ)]/sin^2(γ)
But, cos(γ) = [a^2+b^2-c^2]/2ab = [c^2(k-1)]/2ab (Given a^2+b^2=kc^2)
∴ cot(γ)/[cot(α)+cot(β)] = [c^2(k-1)sin(α)sin(β)]/[2absin^2(γ)]
Since sin(α)/a = sin(β)/a = sin(γ)/c;
cot(γ)/[cot(α)+cot(β)] = [c^2(k-1)]/2 x sin(γ)/c x sin(γ)/c x 1/sin^2(γ) = (k-1)/2
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon - Advanced Level
 Show that any positive integer in base 10 can be represented in base 2 notation$ \\ \\ $ii) Show that$ \ 0.00011001100110011\dots_2 = \frac{1}{10} )
Yes well doneα+β+γ=180 -> cot(α+β)=-cot(γ)
[cot(α)cot(β)-1]/[cot(α)+cot(β)] = -cot(γ)
cot(γ)/[cot(α)+cot(β)] = cot^2(γ)/[cot(α)cot(β)-1] = [-sin(α)sin(β)cos^2(γ)]/[sin^2(γ)cos(α+β)] = [sin(α)sin(β)cos(γ)]/sin^2(γ)
But, cos(γ) = [a^2+b^2-c^2]/2ab = [c^2(k-1)]/2ab (Given a^2+b^2=kc^2)
∴ cot(γ)/[cot(α)+cot(β)] = [c^2(k-1)sin(α)sin(β)]/[2absin^2(γ)]
Since sin(α)/a = sin(β)/a = sin(γ)/c;
cot(γ)/[cot(α)+cot(β)] = [c^2(k-1)]/2 x sin(γ)/c x sin(γ)/c x 1/sin^2(γ) = (k-1)/2
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
We have m=2n or m=2n+1 for some non-negative integer n < m.
But since n < m, n must have a binary representation. We append 0 or 1 to this binary representation to obtain one for m.
ii)x=11.\overline{0011}_2-0.\overline{0011}_2=11_2=3 \Rightarrow x=\frac{1}{10}.)
i) Suppose (for the sake of contradiction) that m is the least positive integer that cannot be written in base 2.Yes well done
 Show that any positive integer in base 10 can be represented in base 2 notation$ \\ \\ $ii) Show that$ \ 0.00011001100110011\dots_2 = \frac{1}{10} )
We have m=2n or m=2n+1 for some non-negative integer n < m.
But since n < m, n must have a binary representation. We append 0 or 1 to this binary representation to obtain one for m.
ii)
aDimitri
i'm the cook
Re: HSC 2014 4U Marathon - Advanced Level

SilentWaters
Member
- Joined
- Mar 20, 2014
- Messages
- 55
- Gender
- Male
- HSC
- 2014
Last edited:
Stygian
Active Member
- Joined
- Aug 11, 2014
- Messages
- 120
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2014 4U Marathon - Advanced Level
i might have a better look at this later
from a brief look at this and a bit of brainstorming, would you use the property of the difference between two squares so like a^2-b^2=(a+b)(a-b) and then show that (17m^2+4n^2)-(17n^2+4m^2) cannot be expressed in that form?
i might have a better look at this later
aDimitri
i'm the cook
Re: HSC 2014 4U Marathon - Advanced Level
(\sqrt{17m^{2} + 4n^{2}} - \sqrt{17n^{2} + 4m^{2}} ) )
You would have to then show that a and b cant both be integers.
It can be expressed in that form though.from a brief look at this and a bit of brainstorming, would you use the property of the difference between two squares so like a^2-b^2=(a+b)(a-b) and then show that (17m^2+4n^2)-(17n^2+4m^2) cannot be expressed in that form?
i might have a better look at this later
You would have to then show that a and b cant both be integers.
- Status
- Not open for further replies.