-
Looking for HSC notes and resources? Check out our Notes & Resources page
HSC 2015 MX2 Marathon ADVANCED (archive) (3 Viewers)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2015 4U Marathon - Advanced Level
Then LHS=[(x+y-z)/z+(x+z-y)/y+(y+z-x)/x]/2=[(x/y+y/x)+(x/z+z/x)+(y/z+z/y)-3]/2 >= 3/2.
(We used AM-GM thrice in the last inequality to bound the (t+1/t) terms below by 2.)
Let x=a+b, y=a+c, z=b+c.
Then LHS=[(x+y-z)/z+(x+z-y)/y+(y+z-x)/x]/2=[(x/y+y/x)+(x/z+z/x)+(y/z+z/y)-3]/2 >= 3/2.
(We used AM-GM thrice in the last inequality to bound the (t+1/t) terms below by 2.)
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2015 4U Marathon - Advanced Level


 = \frac{x}{1-x} \geq \frac{9}{4}x - \frac{1}{4} \\ $(found by considering the tangent to the graph at$ \ x = \frac{1}{3} \ $ then proving the inequality via calculus)$ )
 + f(y) + f(z) \geq \frac{9}{4} (x+y+z) - \frac{3}{4} = \frac{3}{2} \ \square )
nice method, mine was a little longer:Let x=a+b, y=a+c, z=b+c.
Then LHS=[(x+y-z)/z+(x+z-y)/y+(y+z-x)/x]/2=[(x/y+y/x)+(x/z+z/x)+(y/z+z/y)-3]/2 >= 3/2.
(We used AM-GM thrice in the last inequality to bound the (t+1/t) terms below by 2.)
Last edited:
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 463
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon - Advanced Level
that seems familiar to a question in the maths competition by AMT last year. couldnt do it lolsuppose that a polynomial with integer coefficients satisfies P(100)=100. Find the maximum of integer solutions to P(k)=k^3 such a polynomial can have.
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2015 4U Marathon - Advanced Level
Are these polynomials definitely required to have integer coefficients?
Is it definitely P(100)=100?
Are we meant to find the maximum number of solutions to f(k) = k^3 possible, or the largest possible k such that f(k)=k^3?
(I just want to be clear the problem is correctly written before spending time on it.)
Can you please clarify the exact question statement?suppose that a polynomial with integer coefficients satisfies P(100)=100. Find the maximum of integer solutions to P(k)=k^3 such a polynomial can have.
Are these polynomials definitely required to have integer coefficients?
Is it definitely P(100)=100?
Are we meant to find the maximum number of solutions to f(k) = k^3 possible, or the largest possible k such that f(k)=k^3?
(I just want to be clear the problem is correctly written before spending time on it.)
Re: HSC 2015 4U Marathon - Advanced Level
a polynomial is called self centered if it has integer coefficients and p (100) = 100. if p (x) is a self centred polynomial, what is the maximum number of integer solutions to p (k) =k^3?Can you please clarify the exact question statement?
Are these polynomials definitely required to have integer coefficients?
Is it definitely P(100)=100?
Are we meant to find the maximum number of solutions to f(k) = k^3 possible, or the largest possible k such that f(k)=k^3?
(I just want to be clear the problem is correctly written before spending time on it.)
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,650
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon - Advanced Level
 ) ?
?
EDIT: n-2
is the answera polynomial is called self centered if it has integer coefficients and p (100) = 100. if p (x) is a self centred polynomial, what is the maximum number of integer solutions to p (k) =k^3?
EDIT: n-2
Last edited:
Re: HSC 2015 4U Marathon - Advanced Level
nope, I think you've taken a wrong approachis the answer
?
EDIT: n-2
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2015 4U Marathon - Advanced Level
Okay cool, seems hard! Will spend more time on it tomorrow morning, but here is some first progress:
Since P has integer coefficients, we must have k - 100 | P(k) - P(100) = k^3 - 100.
But k^3 - 100 = (k - 100)(k^2 -100k + 10000) + 999900.
So the only k for which the identity P(k) = k^3 can possibly hold true are k such that k - 100 | 999900.
We can prime factorise this large number to obtain (2^2)(3^2)(5^2)(11)(101), which has: 2.3.3.3.2.2=216 integer factors.
So there are at most 216 integers k satisfying the property P(k) = k^3.
It is not clear however, that we can find an INTEGER polynomial passing through the points (k,k^3) for k ranging over the set {100 + d : d | 999900}, so we have only shown that 216 is an upper bound, rather than a maximum.
Will return to this tomorrow.
Okay cool, seems hard! Will spend more time on it tomorrow morning, but here is some first progress:
Since P has integer coefficients, we must have k - 100 | P(k) - P(100) = k^3 - 100.
But k^3 - 100 = (k - 100)(k^2 -100k + 10000) + 999900.
So the only k for which the identity P(k) = k^3 can possibly hold true are k such that k - 100 | 999900.
We can prime factorise this large number to obtain (2^2)(3^2)(5^2)(11)(101), which has: 2.3.3.3.2.2=216 integer factors.
So there are at most 216 integers k satisfying the property P(k) = k^3.
It is not clear however, that we can find an INTEGER polynomial passing through the points (k,k^3) for k ranging over the set {100 + d : d | 999900}, so we have only shown that 216 is an upper bound, rather than a maximum.
Will return to this tomorrow.
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2015 4U Marathon - Advanced Level
Lol, woke up with an idea that I think does it.
Last post we showed that the subset S of k satisfying P(k) = k^3 consists of integers m with 100 - m a divisor of 999900.
We know that P(x) - x^3 vanishes at k in S.
So by the factor theorem we have
 = x^3 + Q(x)\prod_{k\in S} (x-k))
for some integer polynomial Q.
Evaluating at 100, we get:
}=Q(100)\in\mathbb{Z}.)
So we need to find a maximal set of distinct divisors of 999900 with product a factor of 999900.
By inspection, such a set is 1,-1,2,-2,3,-3,5,-5,11,101.
So: Taking Q(x)=-1 as constant and taking S={99,101,98,102,97,103,95,105,89,-1} gives us a concrete expression for an optimal P, and the answer to the question is 10.
(will double-check this in the morning, hopefully no sillies!)
Lol, woke up with an idea that I think does it.
Last post we showed that the subset S of k satisfying P(k) = k^3 consists of integers m with 100 - m a divisor of 999900.
We know that P(x) - x^3 vanishes at k in S.
So by the factor theorem we have
for some integer polynomial Q.
Evaluating at 100, we get:
So we need to find a maximal set of distinct divisors of 999900 with product a factor of 999900.
By inspection, such a set is 1,-1,2,-2,3,-3,5,-5,11,101.
So: Taking Q(x)=-1 as constant and taking S={99,101,98,102,97,103,95,105,89,-1} gives us a concrete expression for an optimal P, and the answer to the question is 10.
(will double-check this in the morning, hopefully no sillies!)
Last edited:
simpleetal
Member
- Joined
- Apr 6, 2015
- Messages
- 54
- Gender
- Male
- HSC
- 2016
Re: HSC 2015 4U Marathon - Advanced Level
here is a great question I was doing a couple of weeks back. show that in every set of 9 positive integers, a subset of 5 positive integers exists such that the sum of the numbers is divisble by 5.
here is a great question I was doing a couple of weeks back. show that in every set of 9 positive integers, a subset of 5 positive integers exists such that the sum of the numbers is divisble by 5.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Re: HSC 2015 4U Marathon - Advanced Level

+ (\frac{b+c}{a+c} + \frac{a+c}{b+c})+ (\frac{c+a}{a+b} + \frac{a+b}{a+c}) \geq 2 + 2+ 2)

 + (\frac{b+c}{a+b}+ \frac{c+a}{a+b})+ (\frac{b+c}{a+c} + \frac{a+b}{a+c}) \geq 6)






Nesbitt's inequality is nice.
Last edited:
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2015 4U Marathon - Advanced Level
(ax+by+cz)^2 <= (a^2+b^2+c^2)(x^2+y^2+z^2)
with equality iff (x,y,z)=(ta,tb,tc) for some real c.
Lots of proofs of Cauchy-Schwartz are on this site, so I will assume it. (Can provide a short proof if you like, such as the one based on non-negative polynomials having non-positive discriminant).
Then C-S implies
LHS^2 =< ((6x+1)+(6y+1)+(6z+1))(1+1+1)=27.
And taking square roots of both sides finishes the question. The C-S equality condition also implies x=y=z=1/3 if we have equality.
Cauchy-Schwartz states for real variables we have:Nesbitt's inequality is nice.

(ax+by+cz)^2 <= (a^2+b^2+c^2)(x^2+y^2+z^2)
with equality iff (x,y,z)=(ta,tb,tc) for some real c.
Lots of proofs of Cauchy-Schwartz are on this site, so I will assume it. (Can provide a short proof if you like, such as the one based on non-negative polynomials having non-positive discriminant).
Then C-S implies
LHS^2 =< ((6x+1)+(6y+1)+(6z+1))(1+1+1)=27.
And taking square roots of both sides finishes the question. The C-S equality condition also implies x=y=z=1/3 if we have equality.
simpleetal
Member
- Joined
- Apr 6, 2015
- Messages
- 54
- Gender
- Male
- HSC
- 2016
Re: HSC 2015 4U Marathon - Advanced Level
Should I post a hint?here is a great question I was doing a couple of weeks back. show that in every set of 9 positive integers, a subset of 5 positive integers exists such that the sum of the numbers is divisble by 5.
simpleetal
Member
- Joined
- Apr 6, 2015
- Messages
- 54
- Gender
- Male
- HSC
- 2016
Re: HSC 2015 4U Marathon - Advanced Level

Or is it the wording of the question that is throwing people off? Here is the exact wording of the question.Should I post a hint?
Last edited:
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Re: HSC 2015 4U Marathon - Advanced Level

[HR][/HR]
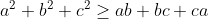
^2 - 2(ab+bc+ca) \geq (a+b+c)^2 - 2(a^2+b^2+c^2))
^2 \leq 3(a^2+b^2+c^2))

[HR][/HR]
^2 \leq 3(6x+1+6y+1+6z+1))



Cauchy-Schwartz states for real variables we have:
(ax+by+cz)^2 (a^2+b^2+c^2)(x^2+y^2+z^2)
with equality iff (x,y,z)=(ta,tb,tc) for some real c.
Lots of proofs of Cauchy-Schwartz are on this site, so I will assume it. (Can provide a short proof if you like, such as the one based on non-negative polynomials having non-positive discriminant).
Then C-S implies
LHS^2 =< ((6x+1)+(6y+1)+(6z+1))(1+1+1)=27.
And taking square roots of both sides finishes the question. The C-S equality condition also implies x=y=z=1/3 if we have equality.
[HR][/HR]
[HR][/HR]
Last edited:
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2015 4U Marathon - Advanced Level
You have some inequalities the wrong way around, idk if your method works exactly but some tweaking might fix it.
[HR][/HR]
[HR][/HR]

SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Re: HSC 2015 4U Marathon - Advanced Level
Yes I will fix it give me a moment.You have some inequalities the wrong way around, idk if your method works exactly but some tweaking might fix it.
- Status
- Not open for further replies.
